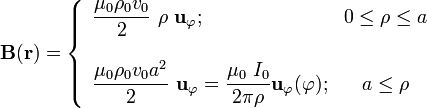Campos eléctricos y magnéticos debidos a un tubo de corriente

De Laplace

(Diferencias entre revisiones)

Revisión de 19:19 13 sep 2008

Contenido

1 Enunciado
2 Solución
- 2.1 Campo eléctrico,
- 2.2 Campo magnético,

1 Enunciado

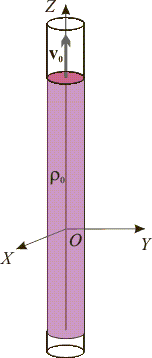
Un cilindro de radio $a$ y longitud infinita posee una densidad de carga uniforme $ρ 0$ . El cilindro se mueve con velocidad constante 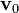$\mathbf{v}_0$ paralelamente a su eje, de forma que existe una densidad de corriente 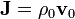$\mathbf{J} = \rho_0\mathbf{v}_0$ . Para todos los puntos del espacio halle:

El campo eléctrico, $\mathbf{E}$ .
El campo magnético, $\mathbf{B}$ .
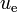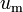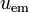Las densidades de energía eléctrica, $u_\mathrm{e}\,$ , magnética, $u_\mathrm{m}\,$ y electromagnética, $u_\mathrm{em}\,$ .
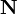El vector de Poynting, $\mathbf{N}$ .
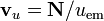La velocidad de propagación de la energía, definida como $\mathbf{v}_u=\mathbf{N}/u_\mathrm{em}$ .

2 Solución

Respecto de un sistema de referencia fijo, el cilindro infinito de radio

a

cargado uniformemente con una densidad de carga eléctrica

ρ 0

, constituye una corriente eléctrica cuando se mueve con una velocidad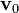 $\mathbf{v}_0$ . Tomando el sistema de referencia con el eje

Z

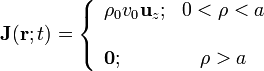
colienal con el eje del cilindro y utilizando las coordenadas cilíndricas $(\rho,\varphi,z)$ , dicha corriente eléctrica estará caracterizada por la densidad volumétrica, $\mathbf{J}(\mathbf{r}; t)=\left\{\begin{array}{lc}\rho_0v_0\mathbf{u}_z; & 0<\rho <a \\ \\ \mathbf{0}; & \rho>a \end{array}\right.$

Como la densidad de carga eléctrica en cada punto de la distribución permanece constante, la corriente que genera su movimiento es estacionaria. Y como tampoco varía en el tiempo, será fuente de un campo magnetostático.

Pero además, consideremos un diferencial fijo de volumen $dτ$ situado en el entorno de un punto $P$ con $ρ < a$ . Como se halla dentro de la región ocupada por la distribución cilíndrica de carga, en cada instante de tiempo existirá en $Δτ$ una cierta cantidad de carga. Obsérvese que ésta permanecerá constante en el tiempo ya que, aunque la carga se está moviendo, las cantidades de carga que entran y salen en $Δτ$ en un diferencial de tiempo son idénticas. Nótese que para que esto ocurra es necesario que la distribución de carga en el cilíndro móvil sea uniforme.

En consecuencia, un observador ligado al sistema de refencia fijo observará en todo momento una distribución estacionaria de carga dada por la densidad,

$\rho_e(\mathbf{r}; t)=\left\{\begin{array}{lc}\rho_0; & 0<\rho <a \\ \\ 0; & \rho>a \end{array}\right.$

que será fuente de un campo eléctrostático 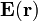$\mathbf{E}(\mathbf{r})$ .

2.1 Campo eléctrico, $\mathbf{E}$

Como se discutió anteriormente, la corriente eléctrica generará un campo magnetostático, por lo que el campo eléctrico existente se deberá exclusivamente a la distribución estática de carga eléctrica que acabamos de describir. Dicho campo es irrotacional y deriva de un potencial electrostático $\phi(\mathbf{r})=\phi(\rho,\varphi,z)$ , en general. Pero dada la simetría cilíndrica de la distribución y su longitud infinita, podemos asegurar que el valor del potencial en un punto sólo va a depender de la distancia $ρ$ al eje $Z$ (eje de la districión de carga), lo que lleva a que el campo eléctrico también va a presentar simetría cilíndrica:

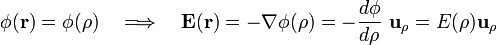
$\phi(\mathbf{r})=\phi(\rho) \quad \Longrightarrow \quad\mathbf{E(r)}=-\nabla \phi(\rho)=-\frac{d\phi}{d\rho}\ \mathbf{u}_\rho=E(\rho) \mathbf{u}_\rho$

A partir de este resultado es fácil determinar la expresión de la intensidad del campo eléctrico mediante la Ley de Gauss. Para ello, consideraremos un recinto cilíndrico $Δτ$ , colineal con la distribución de carga y con radio y altura arbitrarios, $ρ$ y $Δ z$ , respectivamente. El flujo del campo eléctrico a través de la superficie cerrada 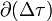$\partial\big(\Delta\tau\big)$ que limita dicho volumen es proporcional a la cantidad de carga eléctrica $Δ Q$ contenida en él. Para una altura $Δ z$ fija, $Δ Q$ va a ser la misma siempre que el radio $ρ$ del volumen $Δτ$ sea mayor que el radio $a$ de la distribución de carga. Sin embargo, si $ρ < a$ , la cantidad de carga contenida es proporcional a cuadrado del radio de $Δτ$ :

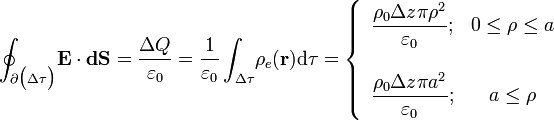
$\oint_{\partial\big(\Delta\tau\big)}\!\mathbf{E\cdot dS}=\frac{\Delta Q}{\varepsilon_0}=\frac{1}{\varepsilon_0}\int_{\Delta\tau}\!\rho_e(\mathbf{r})\mathrm{d}\tau=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0\Delta z\pi\rho^2}{\varepsilon_0};&0\leq\rho\leq a \\ \\ \displaystyle\frac{\rho_0\Delta z\pi a^2}{\varepsilon_0};& a\leq\rho\end{array}\right.$

Por otra parte, puesto que el campo eléctrico tiene la dirección de 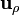$\mathbf{u}_\rho$ en todos los puntos, sólo existirá flujo no nulo a través de la superficie lateral de 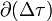$\partial\big(\Delta\tau\big)$ . Igualando el resultado de este cálculo con el anteriormente obtenido para la carga, se determina la expresión del campo eléctrico en todo el espacio:

$\oint_{\partial\big(\Delta\tau\big)}\!\mathbf{E\cdot dS}=\int_0^{2\pi}\!\mathrm{d}\varphi \int_0^{\Delta z}\!E(\rho)\rho\mathrm{d}z=2\pi \Delta z\ \rho\ E(\rho)$ $\Rightarrow$ $\mathbf{E(r)}=E(\rho) \mathbf{u}_\rho=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0}{2\varepsilon_0}\ \rho\ \mathbf{u}_\rho;&0\leq\rho\leq a \\ \\ \displaystyle \frac{\rho_0a^2}{2\varepsilon_0\rho}\ \mathbf{u}_\rho ;& a\leq\rho\end{array}\right.$

2.2 Campo magnético, $\mathbf{B}$

En el sistema bajo estudio no existen materiales con propiedades magnéticas, por tanto, la corriente eléctrica estacionaria y constante producida por el movimiento del cilindro cargado es la única fuente del campo de inducción mangética 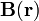$\mathbf{B}(\mathbf{r})$ . Como es bien sabido, una propiedad fundamental de éste es su carácter solenoidal, por lo que deriva de un potencial vector 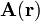$\mathbf{A}(\mathbf{r})$ que depende directamente de las fuentes del campo magnético; en el caso que nos ocupa se tendrá:

$\mathbf{A}(\mathbf{r})= \frac{\mu_0}{4\pi}\ \int_{\mathrm{I\!R}^3} \!\frac{\mathbf{J(r')}\ \mathrm{d}\tau'}{|\mathbf{r}-\mathbf{r}'|}=\mathbf{u}_z \ \frac{\mu_0 \rho_0v_0}{4\pi}\ \int_{\rho<a}\!\frac{\mathrm{d}\tau'}{|\mathbf{r}-\mathbf{r}'|}=A(\rho)\mathbf{u}_z$

No hace falta calcular esta integral pues nos basta con saber que el potencial vector en cualquier punto sólo va a tener componente en la dirección paralela al eje de la distribución. Además, debido a la geometría cilíndrica de la distribución de corriente y su longitud infinita, el valor de dicha componente en un punto arbitrario sólo dependerá de la distancia $ρ$ que lo separa del eje $Z$ . A partir de este resultado es fácil determinar la geometría del campo 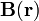$\mathbf{B}(\mathbf{r})$ ,

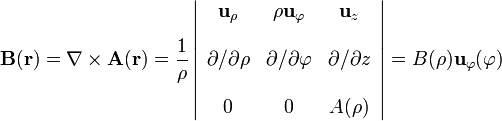
$\mathbf{B}(\mathbf{r})=\nabla\times\mathbf{A}(\mathbf{r})=\frac{1}{\rho}\left|\begin{array} {ccc}\mathbf{u}_{\rho} & \rho \mathbf{u}_{\varphi} & \mathbf{u}_z \\ \\ \partial/\partial\rho & \partial/\partial\varphi & \partial/\partial z \\ \\ 0 & 0 & A(\rho) \end{array}\right|=B(\rho)\mathbf{u}_\varphi(\varphi)$

... así como su expresión en todo el espacio, mediante la aplicación de la Ley de Ampère. Tomemos una circunferencia $\partial\Sigma$ de radio arbitrario

ρ

, centrada en un punto cualquiera del eje

Z

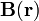y contenida en un plano perpendicular a dicho eje. La Ley de Ampère establece que la circulación del campo $\mathbf{B}(\mathbf{r})$ sobre una curva cerrada $\partial\Sigma$ es proporcional a la intensidad de corriente que atraviesa cualquier superficie que se apoye en dicha curva; por ejemplo, el disco

Σ

de radio

ρ

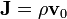. En el caso que nos ocupa, dicha intensidad es el flujo de la densidad $\mathbf{J}=\rho\mathbf{v}_0$ a través de

Σ

, que tendrá el mismo valor

I 0

siempre que el disco sea mayor que la sección transversal del tubo de carga en movimiento, y que será función de

ρ

cuando el valor de este parámetro sea menor que

a

: $\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0\int_\Sigma\!\mathbf{J(r)}\cdot\mathrm{d}\mathbf{S}=\left\{\begin{array}{lc}\mu_0\rho_0v_0\pi\rho^2;& 0\leq \rho\leq a\\ \\ \mu_0\rho_0v_0\pi a^2=\mu_0I_0; & a\leq \rho\end{array}\right.$

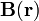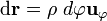Por otra parte, calculamos la circulación del campo $\mathbf{B}(\mathbf{r})$ sobre la curva $\partial\Sigma$ teniendo en cuenta la forma del campo y que el vector elemento de arco sobre la curva es $\mathrm{d}\mathbf{r}=\rho\ d\varphi\mathbf{u}_\varphi$ . Exigiendo que esta circulación debe ser igual a la corriente antes calculada, se obtiene la expresión del campo de inducción magnética:

$\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=2\pi \rho B(\rho)$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})=\left\{\begin{array}{lc}\displaystyle\frac{\mu_0\rho_0v_0}{2}\ \rho\ \mathbf{u}_\varphi; & 0\leq \rho\leq a \\ \\ \displaystyle \frac{\mu_0\rho_0v_0 a^2}{2}\ \mathbf{u}_\varphi =\frac{\mu_0\ I_0}{2\pi\rho}\mathbf{u}_\varphi(\varphi); & a\leq \rho\end{array}\right.$

@@ Línea 63: / Línea 63: @@
 [[Imagen:hilodecorramp.gif|left]]... así como su expresión en todo el espacio, mediante la aplicación de la Ley de Ampère. Tomemos una circunferencia <math>\partial\Sigma</math> de radio arbitrario <math>\rho</math>, centrada en un punto cualquiera del eje <math>Z</math> y contenida en un plano perpendicular a dicho eje. La Ley de Ampère establece que la circulación del campo <math>\mathbf{B}(\mathbf{r})</math> sobre una curva cerrada <math>\partial\Sigma</math> es proporcional a la intensidad de corriente que atraviesa cualquier superficie que se apoye en dicha curva; por ejemplo, el disco <math>\Sigma</math> de radio <math>\rho</math>. En el caso que nos ocupa, dicha intensidad es el flujo de la densidad <math>\mathbf{J}=\rho\mathbf{v}_0</math> a través de <math>\Sigma</math>, que tendrá el mismo valor <math>I_0</math> siempre que el disco sea mayor que la sección transversal del tubo de carga en movimiento, y que será función de <math>\rho</math> cuando el valor de este parámetro sea menor que <math>a</math>:
-<center><math>\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0\int_\Sigma\!\mathbf{J(r)}\cdot\mathrm{d}\mathbf{S}=\left\{\begin{array}{lc}\mu_0\rho_0v_0\pi\rho^2;& 0\leq \rho\leq a\\ \\ \mu_0\rho_0v_0\pi\ a^2=\mu_0I_0; & a\leq \rho\end{array}\right.
+<center><math>\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0\int_\Sigma\!\mathbf{J(r)}\cdot\mathrm{d}\mathbf{S}=\left\{\begin{array}{lc}\mu_0\rho_0v_0\pi\rho^2;& 0\leq \rho\leq a\\ \\ \mu_0\rho_0v_0\pi a^2=\mu_0I_0; & a\leq \rho\end{array}\right.
 </math></center>
@@ Línea 69: / Línea 69: @@
 <center><math>\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=2\pi \rho
-B(\rho)</math>{{tose}}<math style="border:solid red 2px;padding:7px">\mathbf{B}(\mathbf{r})=\left\{\begin{array}{lc}\mu_0\rho_0v_0\pi\rho^2; & 0\leq \rho\leq a\\ \\ \mu_0\rho_0v_0\pi\ a^2=\mu_0I_0; & a\leq \rho\end{array}\right.
+B(\rho)</math>{{tose}}<math style="border:solid red 2px;padding:7px">\mathbf{B}(\mathbf{r})=\left\{\begin{array}{lc}\displaystyle\frac{\mu_0\rho_0v_0}{2}\ \rho\ \mathbf{u}_\varphi; & 0\leq \rho\leq a
-\frac{\mu_0\ I_0}{2
+\\ \\ \displaystyle \frac{\mu_0\rho_0v_0 a^2}{2}\ \mathbf{u}_\varphi =\frac{\mu_0\ I_0}{2\pi\rho}\mathbf{u}_\varphi(\varphi); & a\leq \rho\end{array}\right.</math></center>
-\pi\rho}\mathbf{u}_\varphi(\varphi)</math>
-</center>
 &nbsp;
 [[Categoría:Problemas de ecuaciones de Maxwell]]

Campos eléctricos y magnéticos debidos a un tubo de corriente

De Laplace

Revisión de 19:19 13 sep 2008

Contenido

1 Enunciado

2 Solución

2.1 Campo eléctrico, $\mathbf{E}$

2.2 Campo magnético, $\mathbf{B}$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES