Ciclo de Stirling (GIE)

De Laplace

(Diferencias entre revisiones)

Revisión de 17:04 27 mar 2012

Contenido

1 Enunciado
2 Representación gráfica
3 Trabajo y calor
4 Rendimiento
5 Ciclo con regeneración

1 Enunciado

Un Ciclo de Stirling ideal, sin regeneración, está formado por los siguientes pasos:

Inicialmente tenemos 500 cm³ de aire a 300 K y 100 kPa (estado A)

A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³

B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen.

C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial.

D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial

Para este ciclo.

Indique gráficamente como sería en un diagrama pV.
Calcule el trabajo y el calor que entran en el sistema en cada uno de los cuatro pasos.
Calcule el rendimiento del ciclo.

En un ciclo de Stirling con regeneración, el calor liberado en el proceso D\→A no se pierde sino que se emplea para efectuar el calentamiento en B→C

Calcule el rendimiento del ciclo de Stirling con regeneración. ¿Es mayor o menor que el de una máquina de Carnot que opere entre las mismas temperaturas?

2 Representación gráfica

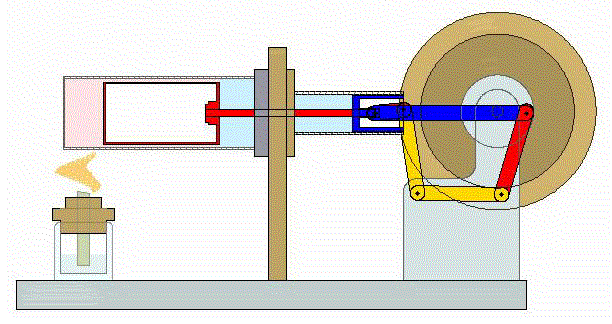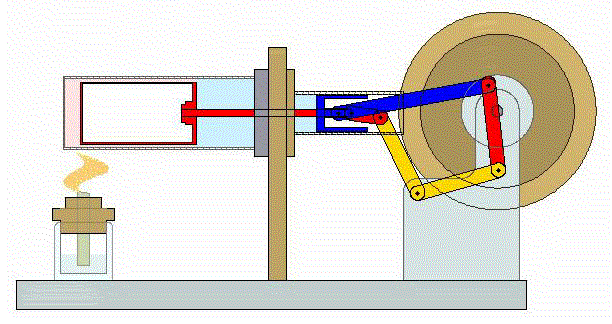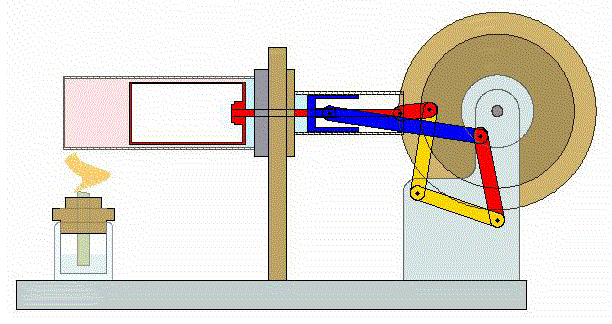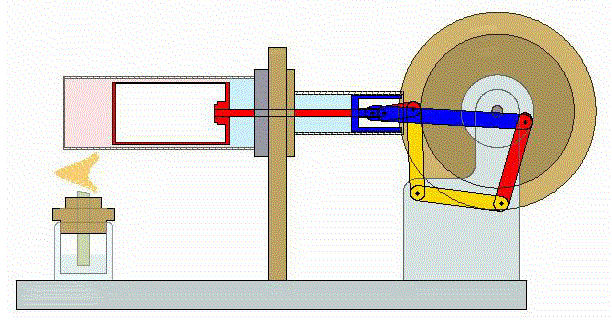
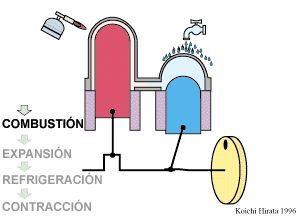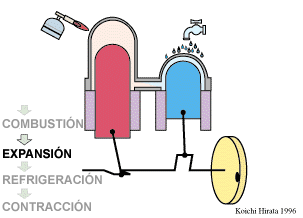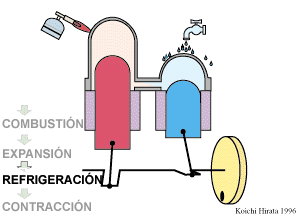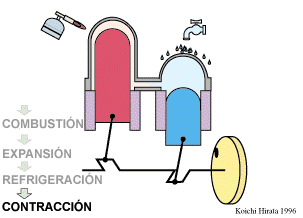
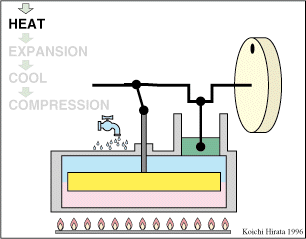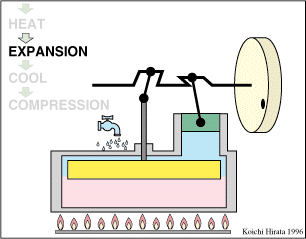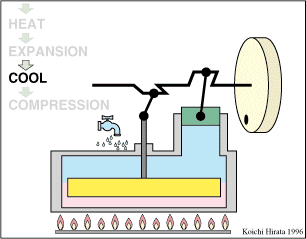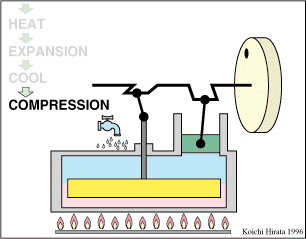
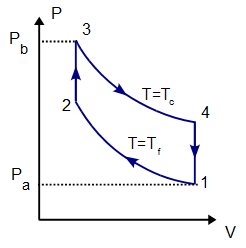
El proceso se compone de cuatro pasos, cuya representación gráfica en un diagrama pV es la siguiente:

A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³. Esto corresponde a un tramo de hipérbola correspondiente a la temperatura indicada.

B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen. Gráficamente, es una línea vertical entre las dos isotermas.

C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial. Otro arco de hipérbola ahora recorrido hacia volúmenes crecientes.

D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial. Es un tramo vertical hacia abajo, cerrando el ciclo.

Los valores de las presiones, temperaturas y volúmenes de cada vértice del ciclo son los siguientes. Partimos del estado A, de cual conocemos las tres magnitudes

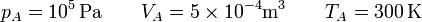
$p_A = 10^5\,\mathrm{Pa}\qquad V_A = 5\times 10^{-4}\mathrm{m}^3\qquad T_A = 300\,\mathrm{K}$

En el estado B tenemos la temperatura y el volumen

$T_B = T_A=300\,\mathrm{K} \qquad V_B = 5\times 10^{-5}\mathrm{m}^3$

y por la ley de los gases ideales hallamos la presión

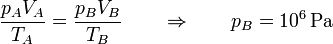
$\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_B = 10^6\,\mathrm{Pa}$

A temperatura constante, si el volumen se divide por 10, la presión se multiplica por el mismo factor.

En el estado C de nuevo tenemos la temperatura y el volumen

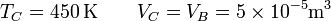
$T_C = 450\,\mathrm{K} \qquad V_C = V_B = 5\times 10^{-5}\mathrm{m}^3$

y hallamos la presión del mismo modo

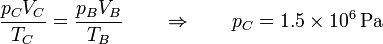
$\frac{p_CV_C}{T_C}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_C = 1.5\times 10^6\,\mathrm{Pa}$

En este caso la temperatura se multiplica por un factor 1.5 y lo mismo ocurre con la presión.

En el último vértice de nuevo tenemos la temperatura y el volumen

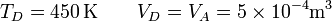
$T_D = 450\,\mathrm{K} \qquad V_D = V_A = 5\times 10^{-4}\mathrm{m}^3$

y resulta la presión

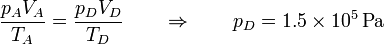
$\frac{p_AV_A}{T_A}=\frac{p_DV_D}{T_D}\qquad\Rightarrow\qquad p_D = 1.5\times 10^5\,\mathrm{Pa}$

Podemos recoger estos estados en la siguiente tabla:

3 Trabajo y calor

4 Rendimiento

En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es

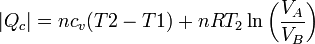
$|Q_c|=nc_v(T2-T1)+nRT_2\ln\left(\frac{V_A}{V_B}\right)$

y del cedido

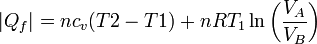
$|Q_f|=nc_v(T2-T1)+nRT_1\ln\left(\frac{V_A}{V_B}\right)$

de forma que el rendimiento es

$\eta = 1 -\frac{|Q_f|}{|Q_c|}= 1- \frac{c_v(T_2-T_1) + RT_1\ln(r)}{c_v(T_2-T_1)+RT_2\ln(r)}$

siendo $r$ la relación de compresión.

Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas

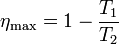
$\eta_\mathrm{max}=1-\frac{T_1}{T_2}$

siendo la diferencia

5 Ciclo con regeneración

@@ Línea 32: / Línea 32: @@
 : '''D&rarr;A''' Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial. Es un tramo vertical hacia abajo, cerrando el ciclo.
+Los valores de las presiones, temperaturas y volúmenes de cada vértice del ciclo son los siguientes. Partimos del estado A, de cual conocemos las tres magnitudes
+<center><math>p_A = 10^5\,\mathrm{Pa}\qquad V_A = 5\times 10^{-4}\mathrm{m}^3\qquad T_A = 300\,\mathrm{K}</math></center>
+En el estado B tenemos la temperatura y el volumen
+<center><math>T_B = T_A=300\,\mathrm{K} \qquad V_B = 5\times 10^{-5}\mathrm{m}^3</math></center>
+y por la ley de los gases ideales hallamos la presión
+<center><math>\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_B = 10^6\,\mathrm{Pa}</math></center>
+A temperatura constante, si el volumen se divide por 10, la presión se multiplica por el mismo factor.
+En el estado C de nuevo tenemos la temperatura y el volumen
+<center><math>T_C = 450\,\mathrm{K} \qquad V_C = V_B = 5\times 10^{-5}\mathrm{m}^3</math></center>
+y hallamos la presión del mismo modo
+<center><math>\frac{p_CV_C}{T_C}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad p_C = 1.5\times 10^6\,\mathrm{Pa}</math></center>
+En este caso la temperatura se multiplica por un factor 1.5 y lo mismo ocurre con la presión.
+En el último vértice de nuevo tenemos la temperatura y el volumen
+<center><math>T_D = 450\,\mathrm{K} \qquad V_D = V_A = 5\times 10^{-4}\mathrm{m}^3</math></center>
+y resulta la presión
+<center><math>\frac{p_AV_A}{T_A}=\frac{p_DV_D}{T_D}\qquad\Rightarrow\qquad p_D = 1.5\times 10^5\,\mathrm{Pa}</math></center>
+Podemos recoger estos estados en la siguiente tabla:
 ==Trabajo y calor==
 ==Rendimiento==

Ciclo de Stirling (GIE)

De Laplace

Revisión de 17:04 27 mar 2012

Contenido

1 Enunciado

2 Representación gráfica

3 Trabajo y calor

4 Rendimiento

5 Ciclo con regeneración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES