Ciclo de Stirling (GIE)
De Laplace
(→Rendimiento) |
(→Representación gráfica) |
||
| Línea 22: | Línea 22: | ||
<center>[[Archivo:EsquemaMotorStirling02.gif]]{{qquad}}{{qquad}}[[Archivo:EsquemaMotorStirling03.gif]]</center> | <center>[[Archivo:EsquemaMotorStirling02.gif]]{{qquad}}{{qquad}}[[Archivo:EsquemaMotorStirling03.gif]]</center> | ||
| + | |||
| + | [[Archivo:ciclo-stirling-01.png|right]] | ||
| + | |||
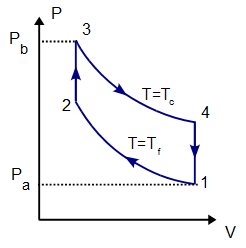
| + | El proceso se compone de cuatro pasos, cuya representación gráfica es la siguiente: | ||
==Trabajo y calor== | ==Trabajo y calor== | ||
Revisión de 16:47 27 mar 2012
Contenido |
1 Enunciado
Un Ciclo de Stirling ideal, sin regeneración, está formado por los siguientes pasos:
Inicialmente tenemos 500 cm³ de aire a 300 K y 100 kPa (estado A)
- A→B Se comprime el gas de forma isoterma, hasta que se reduce su volumen a 50 cm³
- B→C Se calienta el gas hasta una temperatura de 450 K, manteniendo fijado su volumen.
- C→D Se expande el gas a temperatura constante hasta que vuelve a su volumen inicial.
- D→A Se enfría el gas manteniendo constante su volumen hasta que su temperatura vuelve a ser la inicial
Para este ciclo.
- Indique gráficamente como sería en un diagrama pV.
- Calcule el trabajo y el calor que entran en el sistema en cada uno de los cuatro pasos.
- Calcule el rendimiento del ciclo.
En un ciclo de Stirling con regeneración, el calor liberado en el proceso D\→A no se pierde sino que se emplea para efectuar el calentamiento en B→C
- Calcule el rendimiento del ciclo de Stirling con regeneración. ¿Es mayor o menor que el de una máquina de Carnot que opere entre las mismas temperaturas?
2 Representación gráfica
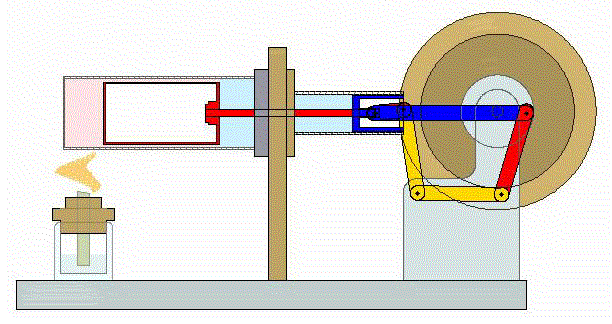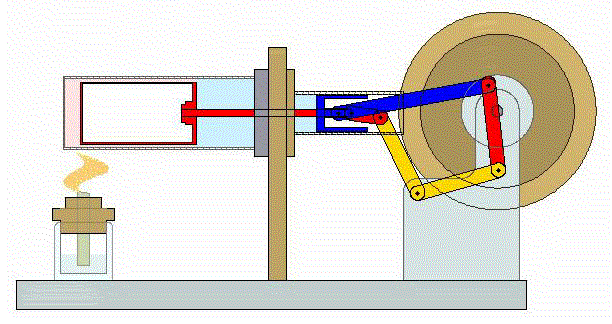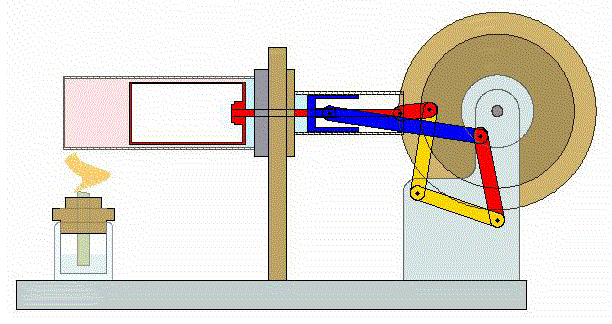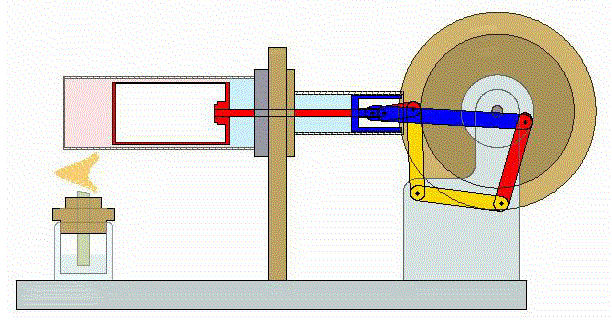
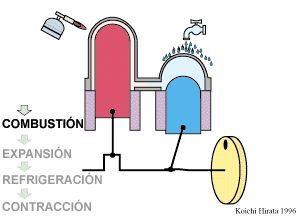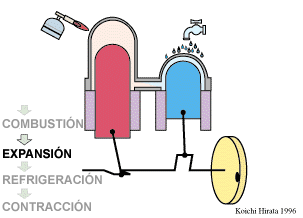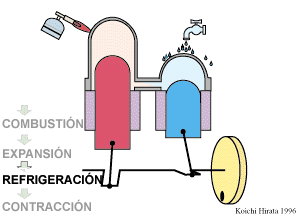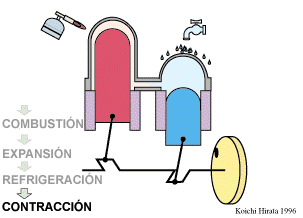
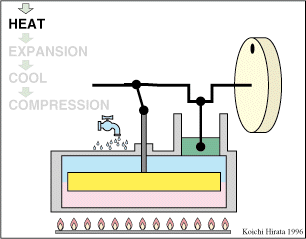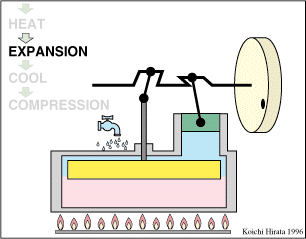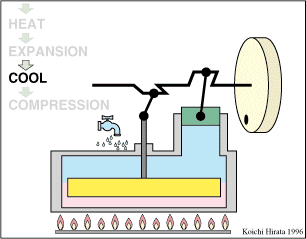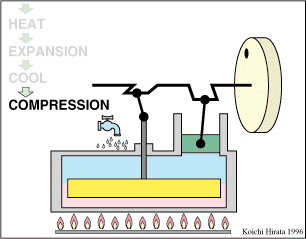
El proceso se compone de cuatro pasos, cuya representación gráfica es la siguiente:
3 Trabajo y calor
4 Rendimiento
En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es
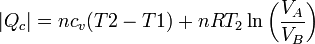
y del cedido
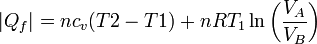
de forma que el rendimiento es

siendo r la relación de compresión.
Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas
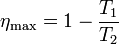
siendo la diferencia