Asociación de dos máquinas térmicas
De Laplace
(→Máquinas ideales) |
(→Máquinas ideales) |
||
| Línea 12: | Línea 12: | ||
Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo | Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo | ||
| - | <center><math>\dot{W}_\mathrm{out1} = \eta_1\,\dot{Q}_\mathrm{ | + | <center><math>\dot{W}_\mathrm{out1} = \eta_1\,\dot{Q}_\mathrm{in1} = \left(1-\frac{T_M}{T_C}\right)\dot{Q}_\mathrm{in1}</math></center> |
que numéricamente tiene el valor | que numéricamente tiene el valor | ||
Revisión de 19:16 17 mar 2012
Contenido |
1 Enunciado
Se tiene una máquina de Carnot que opera entre 1500 K y 600 K recibiendo un flujo de calor 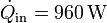 . El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
. El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
Supongamos ahora que en lugar de tratarse de máquinas de Carnot se trata de máquinas reales que tienen un rendimiento del 50\% del máximo posible. ¿Cuál sería en ese caso el rendimiento de la asociación, el calor desechado y el trabajo total realizado? ¿Cuánta entropía se produce a lo largo de un ciclo de la máquina?
2 Máquinas ideales
Consideramos los tres focos térmicos con las temperaturas

Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo
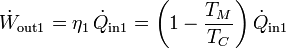
que numéricamente tiene el valor
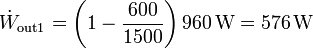
El flujo de calor desechado por esta máquina es

con el valor

Este calor de desecho es el que se usa para alimentar la segunda máquina
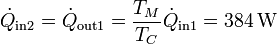
La potencia desarrollada por la segunda máquina la da su rendimiento
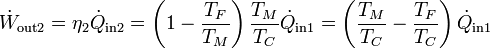
con el valor numérico