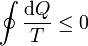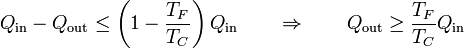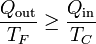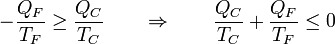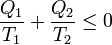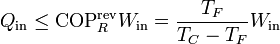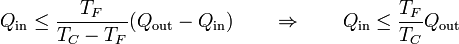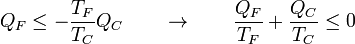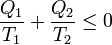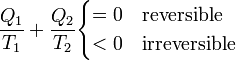|
|
| Línea 72: |
Línea 72: |
| | | | |
| | <center><math>\frac{Q_1}{T_1}+\frac{Q_2}{T_2} \begin{cases} = 0 & \mbox{reversible} \\ < 0 & \mbox{irreversible}\end{cases}</math></center> | | <center><math>\frac{Q_1}{T_1}+\frac{Q_2}{T_2} \begin{cases} = 0 & \mbox{reversible} \\ < 0 & \mbox{irreversible}\end{cases}</math></center> |
| - |
| |
| - | Cump
| |
| - |
| |
| - | Desde el foco caliente entrará en el sistema una cierta cantidad de calor <math>Q_\mathrm{in}</math> y hacia el foco frío saldrá una cantidad <math>Q_\mathrm{out}</math>. Si adoptamos el criterio de que el calor que entra en el sistema es positivo y el que sale es negativo podemos etiquetar cada uno por el foco al que corresponde y escribir
| |
| - |
| |
| - | <center><math>Q_\mathrm{in}=Q_c\qquad\qquad Q_\mathrm{out}=-Q_f</math></center>
| |
| - |
| |
| - | el foco frío una cantidad <math>Q_f</math>. Evidentemente, una de estas dos, o las dos, cantidades será negativa, queriendo decir con ello que el sistema cede calor bien al foco frío (caso de una máquina térmica normal), bien al foco caliente (caso de un [[refrigerador]] o de una [[bomba de calor]]).
| |
| - |
| |
| - | Sobre el sistema se realiza una cierta cantidad de trabajo <math>W</math> que puede ser positivo (caso de un refrigerador o una bomba de calor) o negativo (caso de una máquina térmica).
| |
| - |
| |
| - | ===Ciclo reversible===
| |
| - | Por el [[teorema de Carnot#Corolario|corolario al teorema de Carnot]] se tiene que todas las máquinas reversibles que operen entre las mismas temperaturas tienen el mismo rendimiento. Como todas tienen el mismo puede calcularse analizando algún caso particular, siendo el más sencillo el [[ciclo de Carnot]]. El resultado es que
| |
| - |
| |
| - | <center><math>\eta = 1 - \frac{|Q_f|}{|Q_c|}=1 - \frac{T_f}{T_c}</math></center>
| |
| - |
| |
| - | Restando cada miembro de la unidad queda la igualdad equivalente
| |
| - |
| |
| - | <center><math>\frac{|Q_f|}{|Q_c|} = \frac{T_f}{T_c}</math></center>
| |
| - |
| |
| - | o, equivalentemente,
| |
| - |
| |
| - | <center><math>\frac{|Q_c|}{T_c} = \frac{|Q_f|}{T_f}</math></center>
| |
| - |
| |
| - | Es decir que la cantidad de calor que toma o cede de una fuente es proporcional a la temperatura de dicha fuente.
| |
| - |
| |
| - | En el caso de una máquina térmica, <math>Q_c</math> es positivo, pero el calor <math>Q_f</math> es negativo, por lo que
| |
| - |
| |
| - | <center><math>|Q_f|=-Q_f\,</math>{{tose}}<math>\frac{Q_c}{T_c}=-\frac{Q_f}{T_f}</math></center>
| |
| - |
| |
| - | o, lo que es lo mismo,
| |
| - |
| |
| - | <center><span style="border:blue solid 2px;padding:20px 10px"><math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c} = 0</math></span>{{qquad}}(ciclo reversible)</center>
| |
| - |
| |
| - | En el caso de un refrigerador o de una bomba de calor la cantidad negativa es <math>Q_c</math>, pero el resultado final es el mismo.
| |
| - |
| |
| - | ===Ciclo irreversible===
| |
| - | ====Máquina térmica====
| |
| - | Consideremos un proceso cíclico irreversible que toma calor <math>Q_c</math> de un foco caliente a temperatura <math>T_c</math> y cede una cantidad <math>|Q_f|</math> a un foco frío a temperatura <math>T_f</math>.
| |
| - |
| |
| - | De acuerdo con el teorema de Carnot, el rendimiento de esta máquina térmica será menor que el de una reversible que trabaje entre las mismas dos temperaturas. Esto implica
| |
| - |
| |
| - | <center><math>\eta = 1 -\frac{|Q_f|}{|Q_c|} < \eta_\mathrm{max} = 1 - \frac{T_f}{T_c}</math></center>
| |
| - |
| |
| - | Despejando llegamos a la relación
| |
| - |
| |
| - | <center><math>\frac{|Q_f|}{|Q_c|}>\frac{T_f}{T_c}</math>{{tose}} <math>\frac{|Q_f|}{T_f}> \frac{|Q_c|}{T_c}</math></center>
| |
| - |
| |
| - | El significado físico de este resultado es simple: a igualdad de temperaturas y para el mismo calor tomado del foco caliente, la máquina irreversible produce una cantidad mayor de calor de desecho <math>|Q_f|</math> que una reversible
| |
| - |
| |
| - | Teniendo en cuenta de nuevo que <math>Q_f</math> es negativo queda, finalmente
| |
| - |
| |
| - | <center><math>|Q_f| = -Q_f\,</math>{{tose}}<math>-\frac{Q_f}{T_f}>\frac{Q_c}{T_c}</math>{{tose}}<math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c} < 0</math></center>
| |
| - |
| |
| - | ====Refrigerador====
| |
| - | Puesto que el resultado anterior es una desigualdad hay que tener cuidado con los cambios de signo. Por ello, veamos cómo queda para el caso de que tengamos un refrigerador irreversible. El mismo razonamiento valdrá para una bomba de calor.
| |
| - |
| |
| - | En el caso de un refrigerador lo que nos dice el [[teoremade Carnot#Refrigeradores|teorema de Carnot]] es que el ''coeficiente de desempeño'' (COP) no puede superar al de un refrigerador que funcione según el ciclo de Carnot
| |
| - |
| |
| - | <center><math>\mathrm{COP} = \frac{1}{|Q_c|/|Q_f|-1} < \mathrm{COP}_\mathrm{Carnot} = \frac{1}{T_c/T_f-1}</math></center>
| |
| - |
| |
| - | Despejando
| |
| - |
| |
| - | <center><math>\frac{|Q_c|}{|Q_f|} > \frac{T_c}{T_f}</math> {{tose}} <math>\frac{|Q_c|}{T_c}> \frac{|Q_f|}{T_c}</math></center>
| |
| - |
| |
| - | Físicamente, este resultado nos dice que para extraer la misma cantidad de calor <math>|Q_f|</math> el refrigerador irreversible requiere un trabajo mayor para funcionar y produce una cantidad mayor de calor de desecho (que ahora es <math>|Q_c|</math>).
| |
| - |
| |
| - | Para un refrigerador la cantidad que es negativa es el calor <math>Q_c</math>, por lo que
| |
| - |
| |
| - | <center><math>-\frac{Q_c}{T_c}> \frac{Q_f}{T_c}</math>{{tose}}<math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c}< 0</math></center>
| |
| - |
| |
| - | Este es el mismo resultado que obtuvimos para una máquina térmica irreversible. Por tanto, podemos concluir que
| |
| - |
| |
| - | <center><span style="border:blue solid 2px;padding:20px 10px"><math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c} < 0</math></span>{{qquad}}(ciclo irreversible)</center>
| |
| - |
| |
| - | y, reuniendo ambos resultados
| |
| - |
| |
| - | <center><span style="border:red solid 2px;padding:20px 10px"><math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c} \leq 0</math></span></center>
| |
| - |
| |
| - | cumplíéndose la igualdad para los ciclos reversibles y la desigualdad para los irreversibles.
| |
| - |
| |
| - | ==Enunciado general==
| |
| - | ===Desigualdad de Clausius===
| |
| - | La igualdad y la desigualdad anteriores son válidas para el caso de que haya sólo dos focos térmicos. Pero, ¿qué ocurre si tenemos más de dos?
| |
| - |
| |
| - | Si el sistema evoluciona variando su temperatura en varios pasos, a base de ponerse en contacto con distintos ambientes a diferentes temperaturas, intercambiará calor con cada uno de ellos, y ya no podremos hablar simplemente de <math>Q_c</math> y <math>Q_f</math>, sino que tendremos una serie de calores <math>Q_1</math>, <math>Q_2</math>, <math>Q_3</math>,… que entran en el sistema desde focos a temperaturas <math>T_1</math>, <math>T_2</math>, <math>T_3</math>,….
| |
| - |
| |
| - | En este caso, demostraremos más adelante que la desigualdad correspondiente, conocida como ''desigualdad de Clausius'', es
| |
| - |
| |
| - | <center><math>\frac{Q_1}{T_1}+\frac{Q_2}{T_2}+\frac{Q_3}{T_3}+\cdots \leq 0</math></center>
| |
| - |
| |
| - | donde de nuevo, la igualdad corresponde a ciclos reversibles y la desigualdad a irreversibles.
| |
| - |
| |
| - | Podemos generalizar aun más este resultado: supongamos que la temperatura del ambiente no cambia a saltos, sino que va variando gradualmente de forma continua. Podemos modelar esto como un conjunto infinito de baños térmicos, situados a temperaturas que varían en una cantidad diferencial (por ejemplo, que en un momento está en contacto con un baño a 25.00°C y posteriormente con uno a temperatura 24.99°C).
| |
| - |
| |
| - | La cantidad de calor que entrará en el sistema desde cada uno de estos baños será una cantidad diferencial <math>\mathrm{d}Q</math>. La razón es que si el punto por el que entra el calor ha alcanzado el equilibrio con un baño a 25.00°C y posteriormente se pone en contacto con uno a temperatura 24.99°C, la cantidad de calor que fluirá como consecuencia de la diferencia de temperaturas será minúscula.
| |
| - |
| |
| - | La suma de una cantidad infinita de pasos diferenciales no es más que una integral, por lo que la desigualdad de Clausius se escribe para un proceso continuo como
| |
| - |
| |
| - | <center><span style="border:solid red 2px;padding:20px 10px"><math>\oint\frac{\mathrm{d}Q}{T}\leq 0</math></span></center>
| |
| - |
| |
| - | donde la igualdad corresponde a ciclos reversibles y la desigualdad a irreversibles.
| |
| - |
| |
| - | ===Análisis de la desigualdad===
| |
| - | Para fijar el significado de cada símbolo de la expresión,
| |
| - |
| |
| - | <center><span style="border:solid red 2px;padding:20px 10px"><math>\oint\frac{\mathrm{d}Q}{T}\leq 0</math></span></center>
| |
| - |
| |
| - | precisemos cada uno por separado.
| |
| - |
| |
| - | ; <math>\oint</math>: La integral con el circulito se denomina “integral cerrada” y quiere decir que la suma se efectúa sobre una curva que se cierra sobre sí misma
| |
| - |
| |
| - | ; <math>\mathrm{d}Q</math>: representa la cantidad de calor diferencial que ''entra'' en el sistema desde un foco situado a la temperatura <math>T</math>. A lo largo de un ciclo habrá ocasiones en que su valor sea positivo y veces en que será negativo, según el sistema absorba o ceda calor.
| |
| - |
| |
| - | ; <math>T</math>: es la temperatura del foco que cede el calor. '''No''' es la temperatura del sistema. Es más, para empezar la temperatura del sistema probablemente ni estará definida. En algunos puntos tendrá un valor y en otros será distinto. En el caso de que sí tenga un valor definido, <math>T'\,</math>, este valor será menor que el exterior cuando el calor entra (ya que si no, no entraría), y será mayor que el exterior cuando el calor sale. Solo en un proceso reversible <math>T'\,</math> se diferenciará una cantidad infinitesimal de <math>T</math> (ya que si no, no sería reversible).
| |
| - |
| |
| - | ;<math>\leq 0</math>: La desigualdad de Clausius no nos dice cuanto vale la integral, en general. Solo nos informa de su signo. Pero al hacerlo nos proporciona un criterio para clasificar los posibles procesos:
| |
| - |
| |
| - | :* Si la integral es '''negativa''': el proceso es '''irreversible'''.
| |
| - |
| |
| - | :* Si la integral es '''nula''': el proceso es '''reversible'''.
| |
| - |
| |
| - | :* Si la integral es '''positiva''': el proceso es '''imposible'''.
| |
| - |
| |
| - | ===Demostración del caso general===
| |
| - | [[Imagen:desigualdad-clausius.png|300px|right]]Para demostrar la desigualdad de Clausius partiendo del enunciado de Kelvin-Planck debemos suponer un sistema que realiza un proceso cíclico. En un paso diferencial de dicho ciclo en el sistema entrará una cierta cantidad de calor <math>\mathrm{d}Q</math> y sobre él se realizará un trabajo <math>\mathrm{d}W</math>, de forma que, de acuerdo con el [[Primer Principio]] de la termodinámica
| |
| - |
| |
| - | <center><math>\mathrm{d}U=\mathrm{d}Q+\mathrm{d}W\,</math></center>
| |
| - |
| |
| - | Hay que señalar que esto no presupone que a lo largo de todo el ciclo <math>\mathrm{d}Q</math> vaya a tener siempre el mismo signo. De hecho, en un ciclo real habrá pasos en que entrará calor (del o de los focos calientes), <math>\mathrm{d}Q>0</math> y habrá pasos en que saldrá (hacia el o los focos fríos), <math>\mathrm{d}Q<0</math>, por lo que el signo irá cambiando. Lo mismo ocurrirá con <math>\mathrm{d}W</math>: en un motor real habrá partes del ciclo (el compresor, en una máquina de vapor) en que se realiza trabajo sobre el sistema, <math>\mathrm{d}W>0</math>, y partes (la turbina) en que es el sistema el que realiza el trabajo, <math>\mathrm{d}W<0</math>.
| |
| - |
| |
| - | El calor que entra en el sistema lo hace desde el ambiente a una temperatura <math>T</math>. Esta temperatura no es la temperatura del sistema sino la del foco que cede el calor en ese momento, según se ha indicado anteriormente.
| |
| - |
| |
| - | Para evitar tratar con una infinitud de baños térmicos (uno por cada temperatura por la que pasa el ciclo) podemos sustituir dichos baños por una sola máquina térmica reversible que trabaja entre una temperatura de referencia <math>T_R</math> y la temperatura <math>T</math> con que llega el calor al sistema. Es decir, nos imaginamos que el calor en lugar de entrar desde el ambiente a una temperatura variable, lo hace desde la máquina reversible, que va variando su temperatura de salida. Esta máquina reversible que opera a temperatura variable es por supuesto un ente ideal, pero no afecta a la desigualdad de Clausius y simplifica los cálculos.
| |
| - |
| |
| - | Esta máquina reversible recibe un calor <math>\mathrm{d}Q_R</math> desde el foco a temperatura <math>T_R</math>, y un trabajo <math>\mathrm{d}W_R</math>, y entrega un calor <math>\mathrm{d}Q</math> a la temperatura <math>T</math>. Por ser reversible su cumplirá
| |
| - |
| |
| - | <center><math>\frac{\mathrm{d}Q}{T}=\frac{\mathrm{d}Q_R}{T_R}</math></center>
| |
| - |
| |
| - | Nótese que, puesto que <math>\mathrm{d}Q</math> es el calor que ''entra en el sistema'', debemos contabilizarlo como un calor que ''sale de la máquina'' para que los signos sean coherentes.
| |
| - |
| |
| - | Si consideramos el “sistema ampliado” formado por el sistema y la máquina reversible, se cumple, según el Primer Principio
| |
| - |
| |
| - | <center><math>\mathrm{d}Q_R + \mathrm{d}W_T = \mathrm{d}U_T\,</math></center>
| |
| - |
| |
| - | siendo
| |
| - |
| |
| - | <center><math>\mathrm{d}W_T = \mathrm{d}W+\mathrm{d}W_R\,</math></center>
| |
| - |
| |
| - | el trabajo total realizado sobre el sistema ampliado, y análogamente para la energía interna, para la cual <math>U_T</math> es la suma de la del sistema y de la máquina reversible. En este balance el único calor que entra es <math>\mathrm{d}Q_R</math>, procedente del foco caliente, ya que <math>\mathrm{d}Q</math> se transfiere internamente, no se intercambia con el exterior.
| |
| - |
| |
| - | A lo largo de un ciclo tenemos
| |
| - |
| |
| - | <center><math>\oint \mathrm{d}Q_R+\oint \mathrm{d}W_T = \oint \mathrm{d}U_T</math> {{tose}} <math>Q_R + W_T = 0\,</math></center>
| |
| - |
| |
| - | ya que, por ser la energía interna una función de estado, su valor no cambia en un ciclo completo.
| |
| - |
| |
| - | Ahora bien, el “sistema ampliado” intercambia calor con un solo foco a temperatura <math>T_R</math>. De acuerdo con el [[enunciado de Kelvin-Planck]] la única posibilidad es que entre trabajo y salga calor, y no a la inversa. Por tanto
| |
| - |
| |
| - | <center><math>Q_R = -W_T \leq 0</math></center>
| |
| - |
| |
| - | cumpliéndose la igualdad en el caso reversible y la desigualdad en el irreversible.
| |
| - |
| |
| - | Por otro lado, de que la máquina térmica sea reversible se deduce
| |
| - |
| |
| - | <center><math>\frac{\mathrm{d}Q}{T}=\frac{\mathrm{d}Q_R}{T_R}</math> {{tose}}<math>Q_R = \oint \mathrm{d}Q_R = T_R\oint\frac{\mathrm{d}Q}{T}</math></center>
| |
| - |
| |
| - | y puesto que la temperatura del foco es una cantidad positiva (que no afecta al signo) se llega finalmente a que
| |
| - |
| |
| - | <center><math>Q_R\leq 0</math>{{tose}}<math>\oint\frac{\mathrm{d}Q}{T}\leq 0</math></center>
| |
| - |
| |
| - | que es la desigualdad de Clausius.
| |
| - |
| |
| - | ===El caso de dos focos térmicos===
| |
| - | Puesto que la desigualdad de Clausius se puede tomar como punto de partida para el segundo principio de la Termodinámica, debemos poder deducir de ella todos los resultados conocidos a partir de los otros enunciados.
| |
| - |
| |
| - | Comenzamos por el caso particular de sólo dos focos térmicos. Si el sistema sólo intercambia calor con un baño a temperatura <math>T_c</math> y con otro a temperatura <math>T_f</math>, la integral se puede escribir como
| |
| - |
| |
| - | <center><math>\oint\frac{\mathrm{d}Q}{T} = \int_{T_f}\frac{\mathrm{d}Q}{T}+\int_{T_c}\frac{\mathrm{d}Q}{T}+\int_\mathrm{resto}\frac{\mathrm{d}Q}{T}</math></center>
| |
| - |
| |
| - | En el resto del ciclo no hay intercambio de calor, así que <math>\mathrm{d}Q=0</math> para ese tramo. En los otros dos la temperatura es una constante, por lo que podemos sacarla de la integral y nos queda
| |
| - |
| |
| - | <center><math>\oint\frac{\mathrm{d}Q}{T} = \frac{1}{T_f}\int_{T_f}\mathrm{d}Q+\frac{1}{T_c}\int_{T_c}\mathrm{d}Q+0</math></center>
| |
| - |
| |
| - | la suma de cantidades infinitesimales de calor intercambiadas nos da el calor total intercambiado, por lo que obtenemos finalmente
| |
| - |
| |
| - | <center><math>\oint\frac{\mathrm{d}Q}{T} = \frac{Q_f}{T_f}+\frac{Q_c}{T_c} \leq 0</math></center>
| |
| - |
| |
| - | que es lo que ya conocíamos, pero ahora partiendo de la desigualdad en lugar del Teorema de Carnot.
| |
| - |
| |
| - | ==Relación con otros enunciados==
| |
| - | A partir de la desigualdad es inmediato llegar a los otros enunciados del Segundo Principio.
| |
| - | ===Con el de Kelvin Planck===
| |
| - | [[Imagen:Kelvin-planck.png|296px|right]]
| |
| - |
| |
| - | Para ver que es equivalente al enunciado de Kelvin-Planck nos basta imaginar un proceso en el que no se cumple este enunciado. Supongamos una máquina imaginaria que transforma todo el calor en trabajo. Para esta máquina el calor siempre entra en el sistema, nunca sale de él. Esto quiere decir que <math>\mathrm{d}Q>0</math> en todos los puntos del ciclo. Puesto que la temperatura absoluta es siempre positiva
| |
| - |
| |
| - | <center><math>\mathrm{d}Q > 0\,</math> {{tose}} <math>\oint \frac{\mathrm{d}Q}{T} > 0</math>{{qquad}} (proceso imposible)</center>
| |
| - |
| |
| - | Por tanto, es imposible esta máquina imaginaria y obtenemos el enunciado de Kelvin-Planck.
| |
| - |
| |
| - | ===Con el de Clausius===
| |
| - | [[Imagen:dos-focos.png|296px|right]]Una vez que tenemos el de Kelvin-Planck tenemos el de Clausius, pero veámoslo directamente. Supongamos una máquina imaginaria que, sin requerir trabajo absorbe calor de un foco a temperatura <math>T_2</math> y lo cede a uno a temperatura <math>T_1</math>. Sea <math>|Q|</math> la cantidad transferida. La desigualdad de Clausius para dos focos nos da
| |
| - |
| |
| - | <center><math>Q_2 = +|Q|\,</math>{{qquad}}{{qquad}}<math>Q_1 = -|Q|\,</math>{{qquad}}{{qquad}}<math>\frac{Q_1}{T_1}+\frac{Q_2}{T_2} = |Q|\left(\frac{1}{T_2}-\frac{1}{T_1}\right)\leq 0</math></center>
| |
| - |
| |
| - | Despejando
| |
| - |
| |
| - | <center><math>\frac{1}{T_2}-\frac{1}{T_1}\leq 0</math> {{tose}} <math>T_1-T_2 \leq 0\,</math> {{tose}} <math>T_2 \geq T_1\,</math></center>
| |
| - |
| |
| - | Por tanto, la desigualdad nos conduce a las conclusiones:
| |
| - |
| |
| - | * Si <math>T_2 > T_1</math>, existe una diferencia finita de temperaturas y el calor va del foco caliente al foco frío, de una manera '''irreversible'''.
| |
| - |
| |
| - | * Si <math>T_2 = T_1</math> (la diferencia de temperatura entre los dos focos es infinitesimal) el calor pasa del ambiente al sistema de una forma '''reversible'''.
| |
| - |
| |
| - | * Si <math>T_2 < T_1</math> el proceso es '''imposible'''. No se puede transferir calor del foco frío al foco caliente.
| |
| - |
| |
| - | ===Con el teorema de Carnot===
| |
| - | La demostración del teorema de Carnot es la misma que se describe en el primer apartado, pero en sentido inverso. Si tenemos solo dos focos, y se toma calor <math>Q_c</math> del caliente y se cede <math>|Q_f|</math> al frío la desigualdad de Clausius nos dice que
| |
| - |
| |
| - | <center><math>\frac{Q_c}{T_c}+\frac{Q_f}{T_f} \leq 0</math> {{tose}} <math>\frac{Q_c}{T_c} \leq -\frac{Q_f}{T_f} = \frac{|Q_f|}{T_f}</math></center>
| |
| - |
| |
| - | Intercambiando denominadores
| |
| - |
| |
| - | <center><math>\frac{|Q_f|}{|Q_c|}\geq \frac{T_f}{T_c}</math> {{tose}} <math>\eta = 1 -\frac{|Q_f|}{|Q_c|} \leq 1-\frac{T_f}{T_c}</math></center>
| |
| - |
| |
| - | Distinguiendo los tres casos:
| |
| - |
| |
| - | * Si la máquina es '''irreversible''', su rendimiento es '''menor''' que <math>1 - T_f/T_c</math>.
| |
| - |
| |
| - | * Si la máquina es '''reversible''', su rendimiento es '''igual''' a <math>1 - T_f/T_c</math>.
| |
| - |
| |
| - | * Es '''imposible''' una máquina cuyo rendimiento sea '''mayor''' que <math>1 - T_f/T_c</math>.
| |
| - |
| |
| - | ==Ejemplos==
| |
| - | ===Expansión libre===
| |
| - | Supongamos el siguiente proceso: Un cilindro de volumen total <math>2V_0</math> está dividido en su mitad por un diafragma. A un lado del diafragma hay un gas a temperatura <math>T_0</math> (igual a la del ambiente). Al otro hay vacío. La cámara vacía esta limitada en su extremo por un pistón.
| |
| - |
| |
| - | Se elimina bruscamente el diafragma (por ejemplo, volándolo con un pequeño petardo), de forma que el gas se expande rápidamente hasta llenar el espacio vacío. En esta expansión libre, no se intercambia calor con el exterior, ni tampoco se realiza trabajo sobre el sistema. Por ello la energía interna no cambia y el gas se encuentra a una temperatura final igual a la inicial.
| |
| - |
| |
| - | A continuación se devuelve el gas a su estado inicial, comprimiéndolo con el pistón. La compresión se hace de forma lenta, de forma que puede ir liberando calor y permanecer en todo momento a la temperatura ambiente <math>T_0</math>.
| |
| - |
| |
| - | La desigualdad de Clausius, aplicada a este caso se compone de dos tramos.
| |
| - |
| |
| - | * En la expansión libre no se intercambia calor, <math>\mathrm{d}Q=0</math> y
| |
| - |
| |
| - | <center><math>\int_{V_i}^{V_f}\frac{\mathrm{d}Q}{T} = 0</math></center>
| |
| - |
| |
| - | * En la compresión isoterma, la temperatura permanece constante. La energía interna tampoco cambia, por lo que el trabajo que se va realizando sobre el gas va escapando en forma de calor
| |
| - |
| |
| - | <center><math>0=\mathrm{d}U=\mathrm{d}Q+\mathrm{d}W</math> {{tose}} <math>\mathrm{d}Q = -\mathrm{d}W = p\,\mathrm{d}V</math></center>
| |
| - |
| |
| - | Integrando
| |
| - |
| |
| - | <center><math>\int_{V_f}^{V_i}\frac{\mathrm{d}Q}{T} = \int_{V_f}^{V_i}\frac{\mathrm{d}Q}{T_0}=\int_{V_f}^{V_i}\frac{p}{T_0}\,\mathrm{d}V = nR\int_{V_f}^{V_i}\frac{\mathrm{d}V}{V}= nR\ln\left(\frac{V_i}{V_f}\right)</math></center>
| |
| - |
| |
| - | Sumando las dos contribuciones
| |
| - |
| |
| - | <center><math>\oint \frac{\mathrm{d}Q}{T}=0+nR\ln\left(\frac{V_i}{V_f}\right) < 0</math></center>
| |
| - |
| |
| - | Esta cantidad es negativa puesto que el volumen final es mayor que el inicial. Vemos que el proceso es posible e irreversible, debido a las irreversibilidades mecánicas internas. El proceso inverso (expansión gradual y que luego el gas se comprimiera solo a un volumen menor) es un proceso imposible.
| |
| - |
| |
| - | ===Ciclo reversible===
| |
| - | Para ver el balance en un proceso en el que la temperatura varía gradualmente, supongamos el siguiente ciclo reversible: un gas ideal diatomico contenido en un recipiente rígido de volumen <math>V_i</math> y a una presión <math>p_i</math> (estado A) es calentado gradualmente hasta que su presión es <math>p_f</math> (estado B). En ese momento se libera el pistón y se deja que el gas se expanda adiabáticamente hasta que su presión vuelve a coincidir con la inicial (estado C). Por último, el gas se enfría gradualmente hasta que su volumen coincide con el inicial. Se trata de hallar el volumen máximo que alcanza el gas.
| |
| - |
| |
| - | ;Calentamiento:En el calentamiento gradual suponemos que el sistema se encuentra en contacto sucesivamente con una serie de focos que van entregando calor a temperaturas progresivamente más altas. Esto, por supuesto, es imposible en la práctica. Pero podemos imaginarnos que el ambiente se está calentando gradualmente y arrastra al gas en su subida. En este caso, la cantidad de calor que entra en el gas corresponde a un proceso a volumen constante:
| |
| - |
| |
| - | <center><math>\mathrm{d}Q = nc_V\,\mathrm{d}T</math></center>
| |
| - |
| |
| - | :y la contribución a la integral de Clausius
| |
| - |
| |
| - | <center><math>\int_{A}^{B} \frac{\mathrm{d}Q}{T}= nc_V\int_{A}^B \frac{\mathrm{d}T}{T} = nc_V\ln\left(\frac{T_B}{T_A}\right)</math></center>
| |
| - |
| |
| - | ;Expansión: En la expansión adiabática no hay intercambio de calor con el exterior, por lo que
| |
| - |
| |
| - | <center><math>\int_{B}^{C} \frac{\mathrm{d}Q}{T}= 0</math></center>
| |
| - |
| |
| - | ;Enfriamiento: Por último, el gas se enfría de forma gradual, pero ahora a presión constante
| |
| - |
| |
| - | <center><math>\mathrm{d}Q = nc_p\,\mathrm{d}T</math></center>
| |
| - |
| |
| - | :y el término correspondiente es
| |
| - |
| |
| - | <center><math>\int_{C}^{A} \frac{\mathrm{d}Q}{T}= nc_p\int_{A}^B \frac{\mathrm{d}T}{T} = nc_p\ln\left(\frac{T_A}{T_C}\right)</math></center>
| |
| - |
| |
| - | La suma de las tres contribuciones es
| |
| - |
| |
| - | <center><math>0 = \oint\frac{\mathrm{d}Q}{T}=nc_V\ln\left(\frac{T_B}{T_A}\right)+0 + nc_p\ln\left(\frac{T_A}{T_C}\right)</math></center>
| |
| - |
| |
| - | La suma debe ser igual a cero por tratarse de un ciclo reversible.
| |
| - |
| |
| - | Para obtener una expresión para el volumen máximo, empleamos la ecuación de estado de los gases ideales y nos queda
| |
| - |
| |
| - | <center><math>nc_V\ln\left(\frac{p_BV_B}{p_AV_A}\right)+nc_p\ln\left(\frac{p_AV_A}{p_CV_C}\right) = 0</math></center>
| |
| - |
| |
| - | pero
| |
| - |
| |
| - | <center><math>p_A = p_C</math>{{qquad}}<math>V_A = V_B\,</math></center>
| |
| - |
| |
| - | así que esto se simplifica a
| |
| - |
| |
| - | <center><math>c_V\ln\left(\frac{p_B}{p_C}\right)+c_p\ln\left(\frac{V_B}{V_C}\right) = 0</math></center>
| |
| - |
| |
| - | Dividiendo por <math>c_V</math> y operando con los logaritmos obtenemos
| |
| - |
| |
| - | <center><math>0 = \ln\left(\frac{p_B}{p_C}\right)+\gamma\ln\left(\frac{V_B}{V_C}\right) = \ln\left(\frac{p_BV_B^\gamma}{p_CV_C^\gamma}\right)</math></center>
| |
| - |
| |
| - | Si el logaritmo es nulo, su argumento debe ser igual a la unidad, esto es,
| |
| - |
| |
| - | <center><math>p_BV_B^\gamma = p_CV_C^\gamma</math></center>
| |
| - |
| |
| - | que es la conocida ley de Poisson, pero obtenida empleando la desigualdad de Clausius. El volumen máximo que alcanza será
| |
| - |
| |
| - | <center><math>V_C=V_B\left(\frac{p_B}{p_C}\right)^\frac{1}{\gamma}</math></center>
| |
| - |
| |
| - | Supongamos ahora que la expansión es adiabática, pero irreversible. ¿Se alcanza un valor mayor o menos que este? Sea C' el punto al que llega el émbolo. El razonamiento es idéntico al anterior, salvo que ahora tenemos la desigualdad
| |
| - |
| |
| - | <center><math>\ln\left(\frac{p_B}{p_C}\right)+\gamma\ln\left(\frac{V_B}{V_{C'}}\right) < 0 </math></center>
| |
| - |
| |
| - | Restando la igualdad anterior obtenemos
| |
| - |
| |
| - | <center><math>\gamma\ln\left(\frac{V_C}{V_{C'}}\right) < 0 </math></center>
| |
| - |
| |
| - | que implica
| |
| - |
| |
| - | <center><math>V_{C'} > V_C\,</math></center>
| |
| - |
| |
| - | es decir, que si el proceso es adiabático e irreversible, el pistón finaliza en un volumen mayor. ¿Significa esto que el trabajo realizado por el gas es mayor en el proceso irreversible que en el reversible? No. Realiza ''menos'' trabajo. Al ser un proceso adiabático, el trabajo realizado corresponde a la disminución de energía interna. Por ser menos eficiente, realiza un trabajo menor y la energía final es mayor en el proceso irreversible que en el reversible. Una mayor energía interna corresponde a una mayor temperatura y por tanto a un mayor volumen final. Este caso muestra que, para un proceso irreversible no es cierto que el trabajo es igual a la integral de <math>p\,\mathrm{dV}</math>.
| |
| - |
| |
| - | ==Relación con la entropía==
| |
| - | {{ac|Entropía}}
| |
| - | La desigualdad de Clausius conduce directamente a la definición de entropía. Dado que ese es un tema extenso, en este artículo se indicarán sólo las ideas básicas.
| |
| - | ===Procesos reversibles===
| |
| - | Para un ciclo reversible, la desigualdad se transforma en una igualdad. Si tomamos un ciclo que vaya de un estado <math>1</math> a un estado <math>2</math>, por un cierto camino reversible <math>C</math>, y volvemos por otro también reversible <math>C'</math>, la igualdad se convierte en
| |
| - |
| |
| - | <center><math>\oint\frac{\mathrm{d}Q_\mathrm{R}}{T}=\int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{R}}{T}+\ \ \int_{2\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^1\frac{\mathrm{d}Q_\mathrm{R}}{T}=0</math></center>
| |
| - |
| |
| - | Por ser los caminos reversibles, la integral de 2 a 1 por C' es igual a la integral de 1 a 2 por el mismo camino C', cambiada de signo. Esto implica
| |
| - |
| |
| - | <center><math>\int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{R}}{T} =\ \int_{1\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^2\frac{\mathrm{d}Q_\mathrm{R}}{T}</math></center>
| |
| - |
| |
| - | Puesto que esto es cierto para cualquier otro camino reversible que conecte 1 con 2, concluimos que el valor de la integral es ''independiente del camino'' y por tanto solo depende de los estados inicial y final. Por tanto, su valor es igual a la diferencia de una cierta función de estado que denominamos entropía
| |
| - |
| |
| - | <center><math>\Delta S = S_2 - S_1 = \int_1^2 \frac{\mathrm{d}Q_R}{T}</math></center>
| |
| - |
| |
| - | o, en forma diferencial
| |
| - |
| |
| - | <center><math>\mathrm{d}S = \frac{\mathrm{d}Q_R}{T}</math></center>
| |
| - |
| |
| - | Obsérvese que esta definición sólo nos da el incremento de entropía entre dos estados, no el valor absoluto en cada uno de ellos. Por ello, es preciso definir un estado de referencia a partir del cual se mide la entropía.
| |
| - |
| |
| - | ===Ciclo parcialmente irreversible===
| |
| - | Supongamos ahora un ciclo irreversible formado por un camino irreversible que lleva del estado 1 al 2 y vuelve por un camino reversible. En este caso tenemos la desigualdad
| |
| - |
| |
| - | <center><math>\int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{I}}{T}+\ \ \int_{2\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^1\frac{\mathrm{d}Q_\mathrm{R}}{T}<0</math></center>
| |
| - |
| |
| - | que equivale a decir que la integral por el camino reversible es mayor que por el irreversible
| |
| - |
| |
| - | <center><math>\int_{1\!\!\!\!\!\!\!\!\!\!\!\!\!C'}^2\frac{\mathrm{d}Q_\mathrm{R}}{T} >\ \int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{I}}{T}</math></center>
| |
| - |
| |
| - | Pero la integral por el camino reversible es justamente la diferencia entre la entropía inicial y la final. Por tanto
| |
| - |
| |
| - | <center><math>\Delta S = S_2 -S_1 > \int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{I}}{T}</math></center>
| |
| - |
| |
| - | Podemos transformar esta desigualdad en una igualdad introduciendo la ''producción de entropía'' <math>S_\mathrm{gen}</math>
| |
| - |
| |
| - | <center><math>\Delta S = S_2 -S_1 = \int_{1\!\!\!\!\!\!\!\!\!\!\!\!C}^2\frac{\mathrm{d}Q_\mathrm{I}}{T}+ S_\mathrm{gen}</math></center>
| |
| - |
| |
| - | Por tanto la desigualdad de Clausius equivale a decir que la producción de entropía en un sistema es siempre positiva (en un proceso irreversible) o nula (en uno reversible). Nunca negativa.
| |
| - |
| |
| - | ===Principio del aumento de entropía===
| |
| - | En el caso particular de un sistema aislado, ningún calor entra o sale del sistema, <math>\mathrm{d}Q=0</math> y por tanto
| |
| - |
| |
| - | <center><math>\Delta S_\mathrm{sis} \geq 0</math>{{qquad}}{{qquad}}(sistema aislado)</center>
| |
| - |
| |
| - | esto es, para un sistema aislado la entropía es una función creciente en todo proceso real. Sólo si el proceso es reversible la entropía permanece constante.
| |
| - |
| |
| - | Si consideramos el “universo” como el conjunto del sistema más la parte del ambiente con la que intercambia calor o trabajo, podemos tratar al universo como un sistema aislado, con lo que obtenemos el ''principio del aumento de entropía'':
| |
| - |
| |
| - | <center><span style="border:solid 2px red;padding:10px"><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}\geq 0</math></span>{{qquad}}{{qquad}}(proceso general)</center>
| |
| - |
| |
| - | esto es, en todo proceso real la entropía aumenta (si el proceso es irreversible) o permanece estacionaria (si es reversible), pero nunca disminuye.
| |
| - |
| |
| - | Obsérvese que en un proceso real es posible que la entropía del sistema disminuya (es lo que ocurre normalmente si se enfría), pero esa disminución debe ser compensada por un aumento en el ambiente, que supere con creces dicha disminución.
| |
| | | | |
| | [[Categoría:Segundo principio de la termodinámica (GIE)]] | | [[Categoría:Segundo principio de la termodinámica (GIE)]] |
Al introducir el Segundo Principio de la termodinámica, se formulan varios enunciados que, aunque poseen validez general, están expresados en términos de máquina térmica. Los más importantes de estos enunciados son:
Estos tres enunciados son bastante “concretos” en cuanto a que hablan de procesos y dispositivos fácilmente interpretables. No obstante, el segundo principio de la termodinámica puede enunciarse de formas más abstractas que, si bien requieren un mayor esfuerzo para su interpretación, ponen de manifiesto de forma más clara la validez universal de esta ley.
Antes de enunciar de forma completa y rigurosa la desigualdad de Clausius, conviene presentar y analizar el caso más simple y importante de un sistema en contacto con solo dos focos de temperatura.
Supongamos un dispositivo que realiza un proceso cíclico, tomando calor de un foco caliente y cediéndolo a uno frío. Esto incluye el caso trivial en que no se realice trabajo alguno y se trate de un simple flujo de calor (incluso podría hacerse trabajo sobre el sistema).
De acuerdo con el teorema de Carnot el trabajo realizado en el proceso debe ser menor o igual que el que efectuaría una máquina reversible que operara ente las mismas temperaturas, por lo que
cumpliéndose la igualdad en el caso de que el ciclo sea reversible. Aplicando que el trabajo es la diferencia entre el calor que entra y el que sale, podemos escribir este resultado como una relación entre calores
Esta relación nos dice que el calor expulsado es mayor del que expulsaría un ciclo reversible. Podemos reescribir esta ecuación en la forma
En lugar de la distinción entre calor que entra y calor que sale, podemos asignar el criterio de que todo el calor entra (siendo negativo cuando en realidad sale) y etiquetar cada uno de los dos por el foco al que corresponde. En este caso escribiríamos la identidad anterior como
Si simplemente etiquetamos los focos por 1 y 2, sin distinción de cual tiene más temperatura nos queda la relación simétrica
Podemos operar de forma análoga para el caso de un refrigerador. En este caso, el teorema de Carnot nos dice que el calor que extraemos es menor del que absorberíamos con un refrigerador reversible
Teniendo en cuenta que en este caso el calor entra en el foco frío y sale en el caliente
y etiquetando de nuevo los focos sin distinción de cuál es el frío y cual el caliente
que es exactamente la misma relación que para una máquina térmica.
Si se hace el cálculo correspondiente para una bomba de calor, de nuevo se llega a la misma fórmula.
Por tanto, concluimos que para cualquier dispositivo o proceso cíclico que funcione entre solo dos focos térmicos se verifica la desigualdad