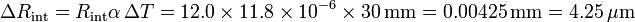Dilatación de una esfera metálica
De Laplace
| Línea 10: | Línea 10: | ||
==Dilatación de los radios== | ==Dilatación de los radios== | ||
| + | Si el cambio de temperatura es pequeño, todas las distancias siguen la misma ley de dilatación | ||
| + | |||
| + | <center><math>L(T) = L_0(1+\alpha (T-T_0))\,</math></center> | ||
| + | |||
| + | o, considerando solo incrementos | ||
| + | |||
| + | <center><math>\Delta L = \alpha L_0\,\Delta T</math></center> | ||
| + | |||
| + | Puesto que los incrementos son usualmente muy pequeños, es preferible trabajar con esta segunda fórmula, ya que en la primera pueden darse errores de redondeo. | ||
| + | |||
| + | El incremento en el radio exterior es | ||
| + | |||
| + | <center><math>\Delta R_\mathrm{ext} = R_\mathrm{ext} \alpha\,\Delta T = 15.0\times 11.8\times 10^{-6} \times 30\,\mathrm{mm} = 0.00531\,\mathrm{mm}= 5.31\,\mu\mathrm{m}</math></center> | ||
| + | |||
| + | Vemos que la dilatación es prácticamente inapreciable, ya que la longitud pasa de 15.0 mm a 15.00531 mm, con lo cual, si se trabaja con tres cifras significativas, este aumento es despreciable y puede ser ignorado. | ||
| + | |||
| + | El radio interior también crece en la misma proporción, es decir, el hueco interior se hace más grande, | ||
| + | |||
| + | <center><math>\Delta R_\mathrm{int} = R_\mathrm{int} \alpha\,\Delta T = 12.0\times 11.8\times 10^{-6} \times 30\,\mathrm{mm} = 0.00425\,\mathrm{mm}= 4.25\,\mu\mathrm{m}</math></center> | ||
| + | |||
| + | |||
==Dilatación en el volumen== | ==Dilatación en el volumen== | ||
==Cambio en la densidad== | ==Cambio en la densidad== | ||
==Presión del gas== | ==Presión del gas== | ||
[[Categoría:Problemas de introducción a la termodinámica (GIE)]] | [[Categoría:Problemas de introducción a la termodinámica (GIE)]] | ||
Revisión de 14:21 3 mar 2012
Contenido |
1 Enunciado
Se tiene una bola hueca de hierro que a 20°C tiene un radio interior de 12.0 mm y un radio exterior de 15.0 mm, siendo la densidad del hierro a esta temperatura 7874 kg/m³ y su coeficiente de dilatación lineal 11.8×10−6K−1.
Se eleva la temperatura de la bola a 50°C. Determine:
- Los nuevos radios interior y exterior de la bola.
- El incremento en el volumen ocupado por el hierro.
- La densidad del hierro a 50°C.
- Si la bola de hierro está llena de aire que inicialmente tiene una presión de 100 kPa, ¿cuál será la presión del gas cuando la esfera está a 50°C?
2 Dilatación de los radios
Si el cambio de temperatura es pequeño, todas las distancias siguen la misma ley de dilatación
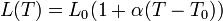
o, considerando solo incrementos
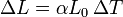
Puesto que los incrementos son usualmente muy pequeños, es preferible trabajar con esta segunda fórmula, ya que en la primera pueden darse errores de redondeo.
El incremento en el radio exterior es
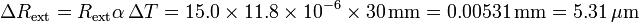
Vemos que la dilatación es prácticamente inapreciable, ya que la longitud pasa de 15.0 mm a 15.00531 mm, con lo cual, si se trabaja con tres cifras significativas, este aumento es despreciable y puede ser ignorado.
El radio interior también crece en la misma proporción, es decir, el hueco interior se hace más grande,