Mezcla de agua y hielo
De Laplace
(→1.0 kg de hielo) |
|||
| Línea 37: | Línea 37: | ||
<center><math>T_f = \frac{m_1 T_1+m_2T_2}{m_1+m_2}-\frac{m_2\,\Delta h_f}{(m_1+m_2)c} = \left(\frac{1.0\cdot 293+0.1\cdot 273}{1.0+0.1}-\frac{0.1\cdot 334}{(1.0+0.1)\cdot 4.18}\right)\mathrm{K} = 284\,\mathrm{K} = 11\,^\circ\mathrm{C}</math></center> | <center><math>T_f = \frac{m_1 T_1+m_2T_2}{m_1+m_2}-\frac{m_2\,\Delta h_f}{(m_1+m_2)c} = \left(\frac{1.0\cdot 293+0.1\cdot 273}{1.0+0.1}-\frac{0.1\cdot 334}{(1.0+0.1)\cdot 4.18}\right)\mathrm{K} = 284\,\mathrm{K} = 11\,^\circ\mathrm{C}</math></center> | ||
| - | == | + | ==Un kilogramo de hielo== |
En el segundo caso podríamos aplicar, en principio, la misma fórmula, cambiando solo la masa de hielo | En el segundo caso podríamos aplicar, en principio, la misma fórmula, cambiando solo la masa de hielo | ||
| Línea 56: | Línea 56: | ||
<center><math>m = -\frac{m_1c(T_f-T_1)}{\Delta h_f} = \frac{83.7\,\mathrm{kJ}}{334\,\mathrm{kJ}/\mathrm{kg}} = 0.251\,\mathrm{kg}</math></center> | <center><math>m = -\frac{m_1c(T_f-T_1)}{\Delta h_f} = \frac{83.7\,\mathrm{kJ}}{334\,\mathrm{kJ}/\mathrm{kg}} = 0.251\,\mathrm{kg}</math></center> | ||
| - | En el estado final tendremos por tanto 749 | + | En el estado final tendremos por tanto 749 g de hielo y 1251 g de agua, ambos a 0°C. |
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
Revisión de 11:47 25 feb 2012
1 Enunciado
Dentro de un recipiente adiabático se sumerge un bloque de 100 g de hielo a 0.0 °C en 1.0 litros de agua a 20 °C. Determine si se funde todo el hielo y la temperatura final del sistema. ¿Qué ocurre si en lugar de 100 g se tiene 1.0 kg de hielo?
2 100 g de hielo
Cuando mezclamos dos fases de una misma sustancia a diferentes temperaturas, se produce un flujo de calor desde la de mayor a la de menor temperatura. Este calor, sin embargo, no se traduce necesariamente en un incremento de temperatura, ya que una parte o todo puede emplearse en un cambio de fase.
Para hallar la solución de esta clase de problemas, a menudo es necesario hacer hipótesis sobre cuál será el estado final del sistema que deben ser revisados posteriormente.
Puesto que el sistema está aislado del exterior, todo el calor es interno, por lo que se cumple la igualdad
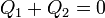
donde llamamos “1” al agua templada y “2” al hielo.
Si la temperatura final del agua es Tf, el calor que entra en ella (que será negativo, porque en realidad sale) es pñroporcional a la variación en su temperatura
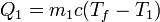
La cantidad máxima de calor que pasa al agua será
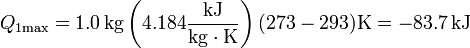
Para el hielo, suponemos que el calor que sale del agua es suficiente para fundirlo por completo y posteriormente incrementar algo su temperatura. Esto es razonable, pues para derretir el hielo necesitamos una cantidad de calor
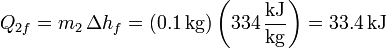
por lo que tenemos de sobra con lo que podemos sacar del agua. En ese caso, el calor total que entra en el hielo será la suma del de fusion más el necesario para elevarlo desde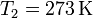 
hasta la temperatura final
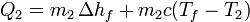
Sumando los dos términos e igualando a cero
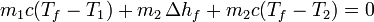
lo que nos da la temperatura final
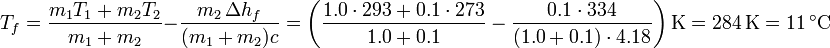
3 Un kilogramo de hielo
En el segundo caso podríamos aplicar, en principio, la misma fórmula, cambiando solo la masa de hielo
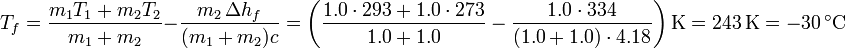
Sin embargo, este resultado es absurdo. No es posible que partiendo de hielo a 0°C y agua a 20°C terminemos con una mezcla a una temperatura inferior a las dos de partida.
El fallo está en suponer que el calor procedente del agua es suficiente para fundir todo el hielo. Como antes, el máximo que podemos sacar del agua antes de que empiece a congelarse es 83.7 kJ, pero ahora se precisan 334 kJ para derretir todo el hielo (pues tenemos 1.0 kg).
Lo que ocurre entonces es que con el calor procedente del agua se funde solo una parte del hielo. Una vez que llega a 0°C el agua alcanza el equilibrio térmico con el hielo y el proceso se detiene. La temperatura final de la mezcla será 0°C. La incógnita es saber cuánto hielo se derrite.
La ecuación para el calor queda en este caso
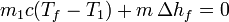
que nos da la masa de hielo que se funde
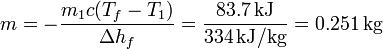
En el estado final tendremos por tanto 749 g de hielo y 1251 g de agua, ambos a 0°C.
