Resorte con rozamiento seco
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se tiene una masa <math>m=5.00\,\mathrm{kg}</math> atada a un resorte de constante <math>k=10.0\,\mathrm{N}/\mathrm{m}</math> y longitud en reposo <math>l_0=150\,\…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
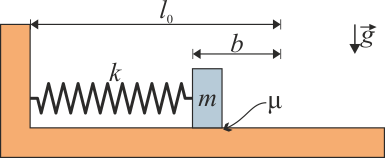
| - | Se tiene una masa <math>m=5.00\,\mathrm{kg}</math> atada a un resorte de constante <math>k=10.0\,\mathrm{N}/\mathrm{ | + | Se tiene una masa <math>m=5.00\,\mathrm{kg}</math> atada a un resorte de constante <math>k=10.0\,\mathrm{N}/\mathrm{cm}</math> y longitud en reposo <math>l_0=150\,\mathrm{mm}</math>. La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento <math>\mu=0.10</math>. El muelle se comprime una cantidad <math>b=50\,\mathrm{mm}</math> respecto a su posición de equilibrio. |
# Despreciando en primer lugar el rozamiento, determine la máxima distancia de la pared a la que llega la masa. | # Despreciando en primer lugar el rozamiento, determine la máxima distancia de la pared a la que llega la masa. | ||
| Línea 7: | Línea 7: | ||
# ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada? | # ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada? | ||
| + | ==Máxima distancia sin rozamiento== | ||
| + | ==Máxima distancia con rozamiento== | ||
| + | ==Posición de la segunda parada== | ||
| + | ==Oscilaciones hasta la detención== | ||
<center>[[Archivo:resorte-pared-rozamiento.png]]</center> | <center>[[Archivo:resorte-pared-rozamiento.png]]</center> | ||
| - | |||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 09:14 20 ene 2012
Contenido |
1 Enunciado
Se tiene una masa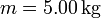 
atada a un resorte de constante 
y longitud en reposo 
. La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento μ = 0.10. El muelle se comprime una cantidad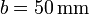 
respecto a su posición de equilibrio.
- Despreciando en primer lugar el rozamiento, determine la máxima distancia de la pared a la que llega la masa.
- Teniendo en cuenta el rozamiento, ¿cuánto vale la distancia de máximo alejamiento?
- Al volver a comprimirse el muelle, la masa no retorna a su posición inicial. ¿A qué distancia de la pared se detiene instantáneamente?
- ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada?
2 Máxima distancia sin rozamiento
3 Máxima distancia con rozamiento
4 Posición de la segunda parada
5 Oscilaciones hasta la detención
