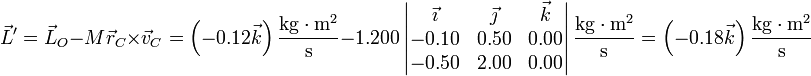Entrar Página Discusión Historial Go to the site toolbox

Ejemplo de sistema de tres partículas

De Laplace

(Diferencias entre revisiones)
(→Centro de masas)
Línea 70: Línea 70:
;Velocidad:
;Velocidad:
<center><math>
<center><math>
-
\vec{v}_C=\frac{m_1\vec{v}_1+m_2\vec{v}_2+m_3\vec{v}_3}{m_1+m_2+m_3} = \frac{0.400(3.00\vec{\jmath})+0.500(-1.20\vec{\imath})+0.300(4.00\vec{\jmath})}{0.400+0.500+0.300}\,\frac{\mathrm{m}}{\mathrm{s}}=\left(-0.5\vec{\imath}+2.00\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+
\vec{v}_C=\frac{m_1\vec{v}_1+m_2\vec{v}_2+m_3\vec{v}_3}{m_1+m_2+m_3} = \frac{0.400(3.00\vec{\jmath})+0.500(-1.20\vec{\imath})+0.300(4.00\vec{\jmath})}{0.400+0.500+0.300}\,\frac{\mathrm{m}}{\mathrm{s}}=\left(-0.50\vec{\imath}+2.00\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
;Aceleración: Operando de la misma forma con las aceleraciones calculadas en el apartado anterior queda
;Aceleración: Operando de la misma forma con las aceleraciones calculadas en el apartado anterior queda

Revisión de 09:56 18 ene 2012

Contenido

1 Enunciado

Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son,

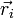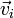i mi (g) \vec{r}_i (m) \vec{v}_i (m/s)
1 400 0.90\vec{\imath} 3.00\vec{\jmath}
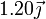
2 500 1.20\vec{\jmath} -1.20\vec{\imath}
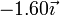
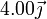
3 300 -1.60\vec{\imath} 4.00\vec{\jmath}

Las tres partículas están conectadas por resortes de longitud natural nula. No hay más fuerzas actuando en el sistema, siendo la constante de los que unen la masa 2 con la 1 y la 2 con la 3 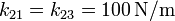k_{21}=k_{23}=100\,\mathrm{N}/\mathrm{m} y el que une la 1 con la 3 k_{13}=32\,\mathrm{N}/\mathrm{m}.

Para el instante indicado:

  1. Determine la aceleración de cada partícula.
  2. Calcule la posición, velocidad y aceleración del CM.
  3. Calcule el momento cinético del sistema respecto al origen y respecto al CM.
  4. Halle la energía cinética del sistema respecto al origen y respecto al CM.
  5. Calcule las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.

2 Aceleraciones

De acuerdo con la segunda ley de Newton, la aceleración de cada masa es proporcional a la resultante de las fuerzas que actúan sobre ella

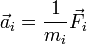
\vec{a}_i = \frac{1}{m_i}\vec{F}_i

En este caso, las fuerzas sobre cada masa son suma de las fuerzas elñasticas, que verifican la ley de Hooke

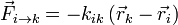
\vec{F}_{i\to k} = -k_{ik}\left(\vec{r}_k-\vec{r}_i\right)

Así nos queda

Masa 1
La aceleración de esta masa vale
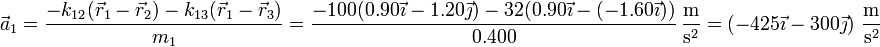
\vec{a}_1 = \frac{-k_{12}(\vec{r}_1-\vec{r}_2)-k_{13}(\vec{r}_1-\vec{r}_3)}{m_1} =\frac{-100(0.90\vec{\imath}-1.20\vec{\jmath})-32(0.90\vec{\imath}-(-1.60\vec{\imath}))}{0.400}\,\frac{\mathrm{m}}{\mathrm{s}^2} = \left(-425\vec{\imath}-300\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}
Masa 2
Para la segunda masa
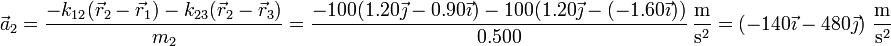
\vec{a}_2 = \frac{-k_{12}(\vec{r}_2-\vec{r}_1)-k_{23}(\vec{r}_2-\vec{r}_3)}{m_2} =\frac{-100(1.20\vec{\jmath}-0.90\vec{\imath})-100(1.20\vec{\jmath}-(-1.60\vec{\imath}))}{0.500}\,\frac{\mathrm{m}}{\mathrm{s}^2} = \left(-140\vec{\imath}-480\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}
Masa 3
Por último
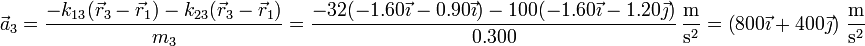
\vec{a}_3 = \frac{-k_{13}(\vec{r}_3-\vec{r}_1)-k_{23}(\vec{r}_3-\vec{r}_1)}{m_3} =\frac{-32(-1.60\vec{\imath}-0.90\vec{\imath})-100(-1.60\vec{\imath}-1.20\vec{\jmath})}{0.300}\,\frac{\mathrm{m}}{\mathrm{s}^2} = \left(800\vec{\imath}+400\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}

3 Centro de masas

La posición, velocidad y aceleración del centro de masas son las respectivas medias ponderadas de las propiedades de las tres partículas.

Posición
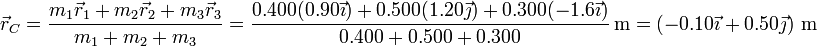
\vec{r}_C=\frac{m_1\vec{r}_1+m_2\vec{r}_2+m_3\vec{r}_3}{m_1+m_2+m_3} = \frac{0.400(0.90\vec{\imath})+0.500(1.20\vec{\jmath})+0.300(-1.6\vec{\imath})}{0.400+0.500+0.300}\,\mathrm{m}=\left(-0.10\vec{\imath}+0.50\vec{\jmath}\right)\,\mathrm{m}
Velocidad
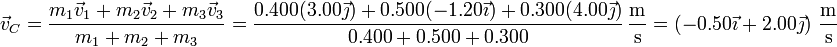
\vec{v}_C=\frac{m_1\vec{v}_1+m_2\vec{v}_2+m_3\vec{v}_3}{m_1+m_2+m_3} = \frac{0.400(3.00\vec{\jmath})+0.500(-1.20\vec{\imath})+0.300(4.00\vec{\jmath})}{0.400+0.500+0.300}\,\frac{\mathrm{m}}{\mathrm{s}}=\left(-0.50\vec{\imath}+2.00\vec{\jmath}\right)\,\frac{\mathrm{m}}{\mathrm{s}}
Aceleración
Operando de la misma forma con las aceleraciones calculadas en el apartado anterior queda
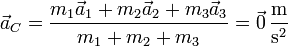
\vec{a}_C=\frac{m_1\vec{a}_1+m_2\vec{a}_2+m_3\vec{a}_3}{m_1+m_2+m_3} = \vec{0}\,\frac{\mathrm{m}}{\mathrm{s}^2}
La aceleración del CM es nula, al ser todas las fuerzas internas y newtonianas.

4 Momento cinético

El momento cinético del sistema respecto a un punto es igual a la suma de los momentos cinéticos respectivos

\vec{L}_O = m_1\vec{r}_1\times\vec{v}_1+m_2\vec{r}_2\times\vec{v}_2+m_3\vec{r}_3\times\vec{v}_3

Sustituyendo cada uno de los valores del enunciado calculamos el momento cinético respecto al origen de coordenadas

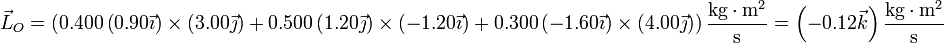
\vec{L}_O = \left(0.400\left(0.90\vec{\imath}\right)\times\left(3.00\vec{\jmath}\right)+0.500\left(1.20\vec{\jmath}\right)\times\left(-1.20\vec{\imath}\right)+0.300\left(-1.60\vec{\imath}\right)\times\left(4.00\vec{\jmath}\right)\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}} = \left(-0.12\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}

Este momento cinético puede descomponerse en la forma

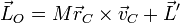
\vec{L}_O = M\vec{r}_C\times\vec{v}_C + \vec{L}'

De aquí podemos despejar el momento cinético respecto al centro de masas

\vec{L}' = \vec{L}_O-M\vec{r}_C\times\vec{v}_C = \left(-0.12\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}-1.200\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -0.10 & 0.50 & 0.00 \\ -0.50 & 2.00 & 0.00 \end{matrix}\right|\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}=\left(-0.18\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}

5 Energía cinética

6 Derivadas temporales

Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplo_de_sistema_de_tres_part%C3%ADculas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace