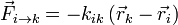Ejemplo de sistema de tres partículas
De Laplace
(Diferencias entre revisiones)
(→Aceleraciones) |
|||
| Línea 45: | Línea 45: | ||
En este caso, las fuerzas sobre cada masa son suma de las fuerzas elñasticas, que verifican la ley de Hooke | En este caso, las fuerzas sobre cada masa son suma de las fuerzas elñasticas, que verifican la ley de Hooke | ||
| - | <center><math>\vec{F}_{i\to k} = -k_{ik}\left(\vec{r}_k-\vec{r}_i | + | <center><math>\vec{F}_{i\to k} = -k_{ik}\left(\vec{r}_k-\vec{r}_i\right)</math></center> |
| + | |||
==Centro de masas== | ==Centro de masas== | ||
==Momento cinético== | ==Momento cinético== | ||
Revisión de 17:57 17 ene 2012
Contenido |
1 Enunciado
Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son,
| i | mi (g) | 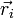 (m) (m)
| 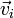 (m/s) (m/s)
|
|---|---|---|---|
| 1 | 400 | 
| 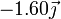
|
| 2 | 500 | 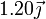
| 
|
| 3 | 300 | 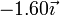
| 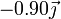
|
Las tres partículas están conectadas por resortes de longitud natural nula. No hay más fuerzas actuando en el sistema, siendo la constante de los que unen la masa 2 con la 1 y la 2 con la 3 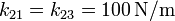 y el que une la 1 con la 3
y el que une la 1 con la 3  .
.
Para el instante indicado:
- Determine la aceleración de cada partícula.
- Calcule la posición, velocidad y aceleración del CM.
- Calcule el momento cinético del sistema respecto al origen y respecto al CM.
- Halle la energía cinética del sistema respecto al origen y respecto al CM.
- Calcule las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.
2 Aceleraciones
De acuerdo con la segunda ley de Newton, la aceleración de cada masa es proporcional a la resultante de las fuerzas que actúan sobre ella
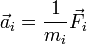
En este caso, las fuerzas sobre cada masa son suma de las fuerzas elñasticas, que verifican la ley de Hooke