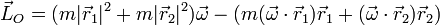Rotores desequilibrados
De Laplace
(→Eje horizontal asimétrico) |
|||
| Línea 22: | Línea 22: | ||
En el primer caso, el desequilibrio se debe a que el centro de masas del sistema no está en el eje de giro. El CM se encuentra a una distancia <math>b</math> del eje y por tanto describe un movimiento circular uniforme con este radio. Al estar acelerado el CM ya la suma de fuerzas aplicadas no es cero, sino que cumple | En el primer caso, el desequilibrio se debe a que el centro de masas del sistema no está en el eje de giro. El CM se encuentra a una distancia <math>b</math> del eje y por tanto describe un movimiento circular uniforme con este radio. Al estar acelerado el CM ya la suma de fuerzas aplicadas no es cero, sino que cumple | ||
| - | <center><math>\vec{\Phi} | + | <center><math>\vec{\Phi}_A+\vec{\Phi}_B = M\vec{a}_C</math></center> |
| - | siendo <math>\vec{\Phi} | + | siendo <math>\vec{\Phi}_A</math> y <math>\vec{\Phi}_B</math> las fuerzas ejercidas por los dos rodamientos en A y B y <math>M = 2m</math> la masa total del sistema. |
En este caso, por la simetría vertical del sistema, las dos fuerzas de los rodamientos son iguales | En este caso, por la simetría vertical del sistema, las dos fuerzas de los rodamientos son iguales | ||
| - | <center><math>\vec{\Phi} | + | <center><math>\vec{\Phi}_A=\vec{\Phi}_B</math></center> |
mientras que la aceleración del CM, como corresponde a un movimiento circular uniforme, es radial y hacia adentro. | mientras que la aceleración del CM, como corresponde a un movimiento circular uniforme, es radial y hacia adentro. | ||
| Línea 40: | Línea 40: | ||
lo que nos da la fuerza ejercida por cada rodamiento | lo que nos da la fuerza ejercida por cada rodamiento | ||
| - | <center><math>\vec{\Phi} | + | <center><math>\vec{\Phi}_A=\vec{\Phi}_B = \frac{M}{2}\vec{a}_c = -m\omega^2b\left(\cos(\omega t)\vec{\imath}+\,\mathrm{sen}(\omega t)\vec{\jmath}\right)</math></center> |
y la fuerza ejercida por el rotor sobre cada uno de los rodamientos será igual a ésta y de sentido contrario | y la fuerza ejercida por el rotor sobre cada uno de los rodamientos será igual a ésta y de sentido contrario | ||
| - | <center><math>\vec{F} | + | <center><math>\vec{F}_A=\vec{F}_B = m\omega^2b\left(\cos(\omega t)\vec{\imath}+\,\mathrm{sen}(\omega t)\vec{\jmath}\right)</math></center> |
| + | |||
| + | Vemos que si <math>b=0</math> y el rotor está centrado, estas fuerzas se anulan. | ||
==Eje inclinado== | ==Eje inclinado== | ||
| + | El segundo caso es más complicado que el primero. En el caso del eje inclinado, el CM se encuentra sobre el eje de rotación. Por tanto, no se mueve y | ||
| + | |||
| + | <center><math>\vec{\Phi}_A+\vec{\Phi}_B = \vec{0}</math></center> | ||
| + | |||
| + | ¿Por qué hay fuerzas de los rodamientos en este caso? Porque aunque la cantidad de movimiento del sistema sea constante, su momento cinético no lo es, y debe haber por tanto un par de fuerzas tal que | ||
| + | |||
| + | <center><math>\vec{M}_O = \vec{r}_A\times\vec{\Phi}_A+\vec{r}_B\times\vec{\Phi}_B = \frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | Pero, ¿por qué el momento cinético varía en el tiempo? Después de todo en este movimiento la velocidad angular es constante y si <math>\vec{L}_O = I\vec{\omega}</math> parecería que si una es constante, el otro también debe serlo. | ||
| + | |||
| + | La razón es que este es un sistema en el que no es cierto lo anterior, sino que | ||
| + | |||
| + | <center><math>\vec{L}_O \neq I\vec{\omega}</math></center> | ||
| + | |||
| + | Puesto que sabemos cómo se mueve cada una de las masas, podemos hallar el valor del momento cinético en cada instante. | ||
| + | |||
| + | Cada masa describe un movimiento circular uniforme, con velocidad | ||
| + | |||
| + | <center><math>\vec{v}=\vec{\omega}\times\vec{r}</math></center> | ||
| + | |||
| + | lo que nos da el momento cinético | ||
| + | |||
| + | <center><math>\vec{L}_O = m\vec{r}_1\times(\vec{\omega}\times\vec{r}_1)+m\vec{r}_2\times(\vec{\omega}\times\vec{r}_2)</math></center> | ||
| + | |||
| + | Desarrollando los dobles productos vectoriales queda | ||
| + | |||
| + | <center><math>\vec{L}_O = (m|\vec{r}_1|^2+m|\vec{r}_2|^2)\vec{\omega} -\left(m(\vec{\omega}\cdot\vec{r}_1)\vec{r}_1+(\vec{\omega}\cdot\vec{r}_2)\vec{r}_2\right)</math></center> | ||
| + | |||
| + | |||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 20:46 8 ene 2012
Contenido |
1 Enunciado
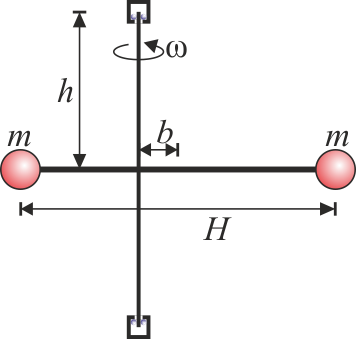
Se tiene un rotor formado por dos masas iguales, de valor m situadas en los extremos de una barra ideal (sin masa) de longitud H. Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia h del centro de la barra (uno por encima y otro por debajo de ella).
Calcule las fuerzas horizontales que el rotor produce sobre los rodamientos cuando gira con velocidad angular constante ω en torno al eje si:
- Es horizontal pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste.
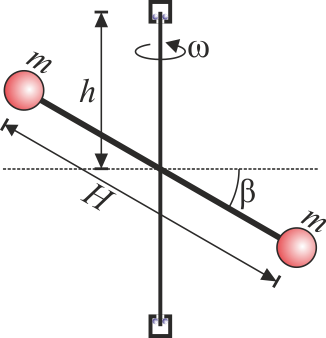
- Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β
Desprecie el efecto del peso.
2 Introducción
El estudio cinemático de este sistema es muy simple: las dos masas describen movimientos circulares uniformes. Podemos hallar fácilmente su posición instantánea, su velocidad y su aceleración. El interés de este sistema se encuentra en el cálculo de las fuerzas que aparecen en él.
En un rotor equilibrado (las dos masas simétricas sobre un eje horizontal) el giro se puede mantener indefinidamente (si no consideramos el rozamiento), sin que haya desgaste sobre los rozamientos.
Si el rotor está desequilibrado, se produce bamboleo y el eje produce fuerzas sobre los rozamientos. Estas fuerzas son además dependientes del tiempo, ya que su dirección gira como las masas, con lo que se produce el fenómeno de la fatiga en el que un sólido experimenta fuerzas oscilantes y periódicas. La fatiga termina por afectar mecánicamente al rodamiento.
En los dos casos considerados aquí, se trata de calcular las fuerzas sobre cada una de los rodamientos. Para ello, calcularemos las fuerzas de reacción ejercidos por estos y, por la tercera ley de Newton, una fuerza igual y de sentido contrario será la ejercida por el rotor.
3 Eje horizontal asimétrico
En el primer caso, el desequilibrio se debe a que el centro de masas del sistema no está en el eje de giro. El CM se encuentra a una distancia b del eje y por tanto describe un movimiento circular uniforme con este radio. Al estar acelerado el CM ya la suma de fuerzas aplicadas no es cero, sino que cumple
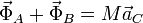
siendo 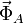 y
y 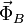 las fuerzas ejercidas por los dos rodamientos en A y B y M = 2m la masa total del sistema.
las fuerzas ejercidas por los dos rodamientos en A y B y M = 2m la masa total del sistema.
En este caso, por la simetría vertical del sistema, las dos fuerzas de los rodamientos son iguales
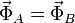
mientras que la aceleración del CM, como corresponde a un movimiento circular uniforme, es radial y hacia adentro.
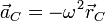
(tomando el origen de coordenadas en el punto de la barra situado en el eje de giro). La posición del CM se encuentra en todo momento a una distancia b del origen. En un sistema de ejes cartesianos se escribe
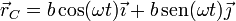
lo que nos da la fuerza ejercida por cada rodamiento
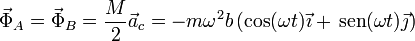
y la fuerza ejercida por el rotor sobre cada uno de los rodamientos será igual a ésta y de sentido contrario
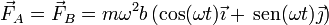
Vemos que si b = 0 y el rotor está centrado, estas fuerzas se anulan.
4 Eje inclinado
El segundo caso es más complicado que el primero. En el caso del eje inclinado, el CM se encuentra sobre el eje de rotación. Por tanto, no se mueve y
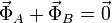
¿Por qué hay fuerzas de los rodamientos en este caso? Porque aunque la cantidad de movimiento del sistema sea constante, su momento cinético no lo es, y debe haber por tanto un par de fuerzas tal que
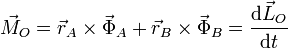
Pero, ¿por qué el momento cinético varía en el tiempo? Después de todo en este movimiento la velocidad angular es constante y si 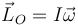 parecería que si una es constante, el otro también debe serlo.
parecería que si una es constante, el otro también debe serlo.
La razón es que este es un sistema en el que no es cierto lo anterior, sino que
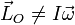
Puesto que sabemos cómo se mueve cada una de las masas, podemos hallar el valor del momento cinético en cada instante.
Cada masa describe un movimiento circular uniforme, con velocidad
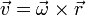
lo que nos da el momento cinético
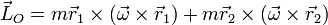
Desarrollando los dobles productos vectoriales queda