Vuelco en un plano inclinado
De Laplace
(→Rozamiento elevado) |
|||
| Línea 55: | Línea 55: | ||
<center><math>mg(b\cos(\alpha)-h\,\mathrm{sen}(\alpha))\geq 0\qquad\Rightarrow\qquad h < b\,\mathrm{cotg}(\alpha)</math></center> | <center><math>mg(b\cos(\alpha)-h\,\mathrm{sen}(\alpha))\geq 0\qquad\Rightarrow\qquad h < b\,\mathrm{cotg}(\alpha)</math></center> | ||
| + | |||
| + | Gráficamente esta condición equivale a que la vertical del peso debe caer dentro de la superficie de la base del bloque. Si cae fuera de ella, el bloque vuelca. | ||
==Rozamiento débil== | ==Rozamiento débil== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 23:43 7 ene 2012
1 Enunciado
Se tiene un bloque en forma de prisma de altura h y base cuadrada de lado b, situado sobre un plano inclinado un ángulo α. Dos de los lados de la base son paralelos a la dirección de descenso del plano (y los otros dos son ortogonales). El coeficiente de rozamiento (estático y dinámico) entre el bloque y el plano vale μ.
Determine el máximo valor de h para que el bloque no vuelque si
- El coeficiente de rozamiento μ > tg(α).
- El coeficiente de rozamiento μ < tg(α).
2 Rozamiento elevado
Cuando el coeficiente de rozamiento es mayor que la pendiente del plano el bloque no desliza, ya que la fuerza de rozamiento es lo bastante intensa como para contrarrestar la componente del peso en la dirección de descenso del plano. Asimismo, la reacción normla del plano compensa la componente del peso normal a él
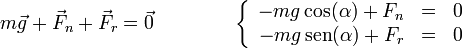
Cuando se considera el bloque no como una partícula, sino como un sólido, es preciso un análisis más detallado. Realmente no hay una sola reacción normal del plano, ni una sola fuerza de rozamiento, sino una infinitud de ellas. En cada punto de contacto entre el sólido y el plano se ejerce una cierta fuerza de reacción y una cierta fuerza de rozamiento.
Lo que vemos como reacción del plano es en realidad la resultante de todas las fuerzas normales
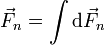
Todas las reacciones tienen en común que son en la dirección del eje Z y van dirigidas hacia z > 0 (ya que el vínculo es unilateral), por lo que se puede escribir
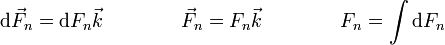
Del mismo modo, la fuerza neta de rozamiento es la resultante de las fuerzas de rozamiento diferenciales

Cuando el bloque se trata como un sólido, no solo debe cumplirse que la suma de fuerzas debe ser nula. Tammbién debe serlo la suma de los momentos respecto a un punto de referencia
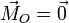
El momento de las fuerzas de reacción sera la resultante de los momentos diferenciales. Si elegimos como punto de referencia la esquina inferior del bloque (respecto de cual se produciría el vuelco, caso de que ocurriera), el momento de las fuerzas de reacción viene dado por una integral
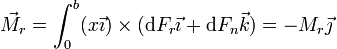
No sabemos cuánto vale esta cantidad (ya que desconocemos cómo está distribuida la fuerza normal) pero sí podemos afirmar que Mr > 0, ya que el producto vectorial del vector de posición de un punto de contacto multiplicado por la fuerza de reacción normal en cada uno de los puntos va en la dirección y sentido de 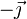 . Dicho en términos físicos, la fuerza de reacción puede impedir que gire hacia dentro del plano (obvio, porque es impenetrable), pero no que gire hacia afuera (ya que no es capaz de retener al sólido).
. Dicho en términos físicos, la fuerza de reacción puede impedir que gire hacia dentro del plano (obvio, porque es impenetrable), pero no que gire hacia afuera (ya que no es capaz de retener al sólido).
La condición de equilibrio de los momentos queda entonces

siendo el momento del peso
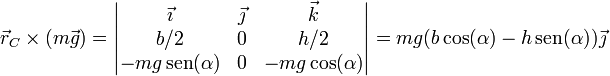
Llevando esto a la ecuación de equilibrio
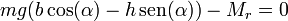
puesto que
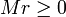
obtenemos la condición para h
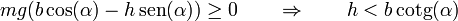
Gráficamente esta condición equivale a que la vertical del peso debe caer dentro de la superficie de la base del bloque. Si cae fuera de ella, el bloque vuelca.





