Vuelco en un plano inclinado
De Laplace
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tiene un bloque en forma de prisma de altura <math>h</math> y base cuadrada de lado <math>b</math>, situado sobre un plano inclinado un ángulo <math>\ | + | Se tiene un bloque en forma de prisma de altura <math>h</math> y base cuadrada de lado <math>b</math>, situado sobre un plano inclinado un ángulo <math>\alpha</math>. Dos de los lados de la base son paralelos a la dirección de descenso del plano (y los otros dos son ortogonales). El coeficiente de rozamiento (estático y dinámico) entre el bloque y el plano vale <math>\mu</math>. |
Determine el máximo valor de <math>h</math> para que el bloque no vuelque si | Determine el máximo valor de <math>h</math> para que el bloque no vuelque si | ||
| - | # El coeficiente de rozamiento <math>\mu > \mathrm{tg}(\ | + | # El coeficiente de rozamiento <math>\mu > \mathrm{tg}(\alpha)</math>. |
| - | # El coeficiente de rozamiento <math>\mu < \mathrm{tg}(\ | + | # El coeficiente de rozamiento <math>\mu < \mathrm{tg}(\alpha)</math>. |
==Rozamiento elevado== | ==Rozamiento elevado== | ||
| + | Cuando el coeficiente de rozamiento es mayor que la pendiente del plano el bloque [[Fuerzas_de_rozamiento_(GIE)#Rozamiento_est.C3.A1tico|no desliza]], ya que la fuerza de rozamiento es lo bastante intensa como para contrarrestar la componente del peso en la dirección de descenso del plano. Asimismo, la reacción normla del plano compensa la componente del peso normal a él | ||
| + | |||
| + | <center><math>m\vec{g} + \vec{F}_n+\vec{F}_r = \vec{0}\qquad\qquad\left\{\begin{array}{rcl} -mg\cos(\alpha)+F_n & = & 0 \\ -mg\,\mathrm{sen}(\alpha)+F_r & = 0& 0 \end{array}\right.</math></center> | ||
| + | |||
| + | Cuando se considera el bloque no como una partícula, sino como un sólido, es preciso un análisis más detallado. Realmente no hay una sola reacción normal del plano, ni una sola fuerza de rozamiento, sino una infinitud de ellas. En cada punto de contacto entre el sólido y el plano se ejerce una cierta fuerza de reacción y una cierta fuerza de rozamiento. | ||
| + | |||
| + | Lo que vemos como ''reacción del plano'' es en realidad la resultante de todas las fuerzas normales | ||
| + | |||
| + | <center><math>\vec{F}_n = \int \mathrm{d}\vec{F}_n</math></center> | ||
| + | |||
| + | Todas las reacciones tienen en común que son en la dirección del eje Z y van dirigidas hacia <math>z>0</math> (ya que el vínculo es unilateral), por lo que se puede escribir | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{F}_n = \mathrm{d}F_n\vec{k}\qquad\qquad \vec{F}_n = F_n\vec{k}\qquad\qquad F_n = \int \mathrm{d}F_n</math></center> | ||
| + | |||
| + | Del mismo modo, la fuerza neta de rozamiento es la resultante de las fuerzas de rozamiento diferenciales | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{F}_r = \mathrm{d}F_r\vec{\imath} \qquad\qquad\vec{F}_r = \int \mathrm{d}\vec{F}_r</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
==Rozamiento débil== | ==Rozamiento débil== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 11:29 7 ene 2012
1 Enunciado
Se tiene un bloque en forma de prisma de altura h y base cuadrada de lado b, situado sobre un plano inclinado un ángulo α. Dos de los lados de la base son paralelos a la dirección de descenso del plano (y los otros dos son ortogonales). El coeficiente de rozamiento (estático y dinámico) entre el bloque y el plano vale μ.
Determine el máximo valor de h para que el bloque no vuelque si
- El coeficiente de rozamiento μ > tg(α).
- El coeficiente de rozamiento μ < tg(α).
2 Rozamiento elevado
Cuando el coeficiente de rozamiento es mayor que la pendiente del plano el bloque no desliza, ya que la fuerza de rozamiento es lo bastante intensa como para contrarrestar la componente del peso en la dirección de descenso del plano. Asimismo, la reacción normla del plano compensa la componente del peso normal a él
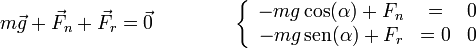
Cuando se considera el bloque no como una partícula, sino como un sólido, es preciso un análisis más detallado. Realmente no hay una sola reacción normal del plano, ni una sola fuerza de rozamiento, sino una infinitud de ellas. En cada punto de contacto entre el sólido y el plano se ejerce una cierta fuerza de reacción y una cierta fuerza de rozamiento.
Lo que vemos como reacción del plano es en realidad la resultante de todas las fuerzas normales
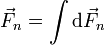
Todas las reacciones tienen en común que son en la dirección del eje Z y van dirigidas hacia z > 0 (ya que el vínculo es unilateral), por lo que se puede escribir
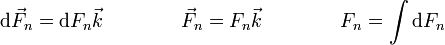
Del mismo modo, la fuerza neta de rozamiento es la resultante de las fuerzas de rozamiento diferenciales






