Cañón casero
De Laplace
(→Solución) |
|||
| Línea 33: | Línea 33: | ||
Si la masa de la bola de acero es mucho menor que la de la pelota de ping-pong, podemos despreciar m frente a M y obtener | Si la masa de la bola de acero es mucho menor que la de la pelota de ping-pong, podemos despreciar m frente a M y obtener | ||
| - | <center><math>v_{2f}\to 3v_i</math></center> | + | <center><math>v_{2f}\to 3v_i\,</math></center> |
es decir, la pelota sale con una rapidez que es el triple de la que tenía al bajar. Esto se traduce en que alcanza una altura máxima | es decir, la pelota sale con una rapidez que es el triple de la que tenía al bajar. Esto se traduce en que alcanza una altura máxima | ||
| Línea 42: | Línea 42: | ||
Por supuesto, en un experimento real sube bastante menos por los efectos ya mencionados de rozamiento con el aire, en las colisiones, y que la proporxión entre las masas no sea infinita. Pero aun así, el dispositivo se puede fabricar para producir saltos lanzamientos bastante vistosos. | Por supuesto, en un experimento real sube bastante menos por los efectos ya mencionados de rozamiento con el aire, en las colisiones, y que la proporxión entre las masas no sea infinita. Pero aun así, el dispositivo se puede fabricar para producir saltos lanzamientos bastante vistosos. | ||
| - | |||
| - | |||
| - | |||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
Revisión de 21:29 15 dic 2011
1 Enunciado
Se puede construir un sencillo cañón casero para disparos en vertical de la siguiente manera: se toma un tubo vertical de longitud L (tómese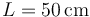 
) cuyo extremo inferior se apoya en el suelo. Por su interior se dejan caer prácticamente seguidas dos bolas, siendo la inferior mucho más pesada que la superior (por ejemplo, una bola de acero y una pelota de ping-pong). Estime la altura máxima a la que subiría la bola ligera tras los rebotes. Justifique las aproximaciones que se efectúen.
2 Solución
Describamos en primer lugar lo que ocurre: por un tubo dejamos caer las dos bolas casi seguidas, siendo la más pesada la inferior; cuando llegan al fondo del tubo, la pesada rebota en el suelo y comienza a ascender; en ese momento colisiona con la bola ligera que aun está descendiendo. Como resultado, la pelota de ping-pong sale disparada hacia arriba.
Puesto que se trata de estimar la altura máxima a la que asciende, podemos despreciar el efecto de las fuerzas de rozamiento, ya que estas lo único que harán será disipar energía y por tanto reducir la altura que alcanza la pelota ligera.
Por la misma razón, consideraremos que las colisiones son elásticas y tampoco se pierde energía en ellas.
Esto no quiere decir que en un experimento real estas fuerzas y efectos sean despreciables, sino que en un experimento real, la altura a la que subirá la pelota será menor que la que obtengamos aquí.
Cuando soltamos las dos bolas, las dos bolas llegan al fondo del tubo con una velocidad de impacto
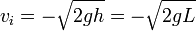
siendo esta velocidad negativa ya que las bolas están descendiendo y suponemos el movimiento rectilíneo, con el eje Z vertical y hacia arriba.
Cuando la bola de acero rebota elásticamente en el fondo, empieza a ascender con la misma rapidez que llevaba. En ese momento choca con la pelota, que baja con la misma velocidad de impacto (habría una pequeña diferencia, por la diferencia en la altura recorrida, pero si las bolas son pequeñas y se han dejado caer casi seguidas, podemos suponer que esta distancia es despreciable).
En esta colisión se conserva la cantidad de movimiento, de forma que
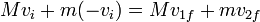
Si el choque es elástico el coeficiente de restitución es la unidad, lo que implica
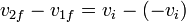
Resolviendo este sistema de dos ecuaciones con dos incógnitas obtenemos, para la velocidad de la pelota,
Si la masa de la bola de acero es mucho menor que la de la pelota de ping-pong, podemos despreciar m frente a M y obtener
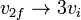
es decir, la pelota sale con una rapidez que es el triple de la que tenía al bajar. Esto se traduce en que alcanza una altura máxima
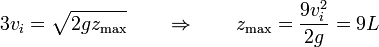
es decir, que la bola pequeña subiría hasta una altura de 9 veces la longitud del tubo (en este caso serían 4.5 metros).
Por supuesto, en un experimento real sube bastante menos por los efectos ya mencionados de rozamiento con el aire, en las colisiones, y que la proporxión entre las masas no sea infinita. Pero aun así, el dispositivo se puede fabricar para producir saltos lanzamientos bastante vistosos.
