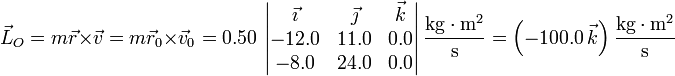Conservación en un oscilador armónico tridimensional
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula de masa <math>m=0.50\,\mathrm{kg}</math> se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke <center><math>\vec{F}=-k\v…') |
|||
| Línea 13: | Línea 13: | ||
==Momento cinético== | ==Momento cinético== | ||
| + | El momento cinético de la partícula es una constante de movimiento, por tratarse de una fuerza central. Su valor lo obtenemos a partir de la posición y la velocidad iniciales | ||
| + | |||
| + | <center><math>\vec{L}_O=m\vec{r}\times\vec{v} = m\vec{r}_0\times\vec{v}_0 = 0.50\,\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -12.0 & 11.0 & 0.0 \\ -8.0 & 24.0 & 0.0\end{matrix}\right|\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}=\left(-100.0\,\vec{k}\right)\frac{\mathrm{kg}\cdot\mathrm{m}^2}{\mathrm{s}}</math></center> | ||
| + | |||
==Energía mecánica== | ==Energía mecánica== | ||
==Distancias y velocidades extremas== | ==Distancias y velocidades extremas== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 14:54 4 dic 2011
Contenido |
1 Enunciado
Una partícula de masa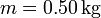 
se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke
siendo su posición y velocidad iniciales
- Calcule el momento cinético de la partícula respecto al origen de coordenadas
- Halle la energía mecánica de la partícula
- Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza
2 Momento cinético
El momento cinético de la partícula es una constante de movimiento, por tratarse de una fuerza central. Su valor lo obtenemos a partir de la posición y la velocidad iniciales
