Velocidad de escape (GIE)
De Laplace
(→Caso terrestre, lunar y marciano) |
|||
| Línea 35: | Línea 35: | ||
|- | |- | ||
| Tierra | | Tierra | ||
| - | | 398& | + | | 398 600.4418 |
| 6 370 | | 6 370 | ||
|- | |- | ||
| Luna | | Luna | ||
| - | | | + | | 4%thinsp;902.7779 |
| 1 737 | | 1 737 | ||
|- | |- | ||
| Línea 50: | Línea 50: | ||
| 695 500 | | 695 500 | ||
|} | |} | ||
| + | |||
| + | Esto da las siguientes velocidades de escape: | ||
| + | |||
| + | ;Tierra: | ||
| + | |||
| + | <center><math>v = \sqrt{\frac{2GM_T}{R_T}}=11.2\,\frac{\mathrm{km}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ;Luna: | ||
| + | |||
| + | <center><math>v = \sqrt{\frac{2GM_L}{R_L}}=2.38\,\frac{\mathrm{km}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ;Marte: | ||
| + | |||
| + | <center><math>v = \sqrt{\frac{2GM_M}{R_M}}=5.03\,\frac{\mathrm{km}}{\mathrm{s}}</math></center> | ||
| + | |||
En el caso de un cohete que parte de la superficie terrestre <math>r = R_T</math>. El valor de <math>GM</math> lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre | En el caso de un cohete que parte de la superficie terrestre <math>r = R_T</math>. El valor de <math>GM</math> lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre | ||
| Línea 56: | Línea 71: | ||
Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol. | Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol. | ||
| - | |||
| - | |||
==Agujero negro clásico== | ==Agujero negro clásico== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 21:33 26 nov 2011
Contenido |
1 Enunciado
Se define la velocidad de escape de un campo gravitatorio como aquella que permite llegar al infinito con velocidad nula. Sabiendo que la energía potencial gravitatoria tiene la expresión
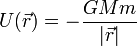
- Determine la velocidad de escape que debe tener un cuerpo para salir de la superficie terrestre hacia el espacio exterior.
- Halle los valores numéricos para el caso de la superficie terrestre, la lunar y la marciana (consulte los datos de las masas en internet).
- Determine el radio que debería tener el Sol para que ni la luz pudiera escapar de él.
2 Velocidad de escape
La velocidad de escape se define como la mínima velocidad que es preciso comunicar a un cuerpo ligero para salir del campo gravitatorio de otro masivo.
Esta velocidad mínima es la que permite llegar al infinito con velocidad nula. Una velocidad menor no permitiría salir del “pozo” de energía potencial gravitatoria.
La energía mecánica de una partícula en un campo gravitatorio es
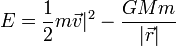
Imponiendo que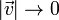 
cuando 
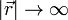queda
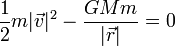
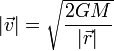
Aquí r es la distancia de partida, que usualmente será igual al radio del planeta
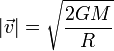
3 Caso terrestre, lunar y marciano
El valor del producto GM es conocido con mayor precisión que el valor de la constante de gravitación universal y que la masa de cada planeta por separado. El radio medio de la Tierra, Luna y Marte también es conocido con precisión. El radio del Sol es más incierto, por tratarse de una esfera gaseosa. Así tenemos
| Cuerpo | GM (km³/s²) | R (km) |
|---|---|---|
| Tierra | 398 600.4418 | 6 370 |
| Luna | 4%thinsp;902.7779 | 1 737 |
| Marte | 42 828 | 3 386 |
| Sol | 132 712 440 018 | 695 500 |
Esto da las siguientes velocidades de escape:
- Tierra
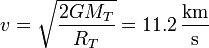
- Luna
- Marte
En el caso de un cohete que parte de la superficie terrestre r = RT. El valor de GM lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre
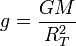
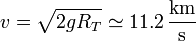
Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol.
