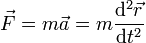Fuerza en anilla ensartada en varillas
De Laplace
(Diferencias entre revisiones)
| Línea 5: | Línea 5: | ||
==Sin considerar el peso== | ==Sin considerar el peso== | ||
| + | [[Anilla_ensartada_en_dos_varillas_(GIE)|Conocemos el movimiento]] de la anilla: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular <math>2\Omega</math> y el radio de giro <math>L/2</math>. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda, | ||
| + | |||
| + | <center><math>\vec{r}(t) = L\cos^2(\Omega t)\vec{\imath}+L\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{\jmath}</math></center> | ||
| + | |||
| + | La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton | ||
| + | |||
| + | <center><math>\vec{F}=m\vec{a}=m\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}</math></center> | ||
==Incluyendo el peso== | ==Incluyendo el peso== | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 10:50 26 nov 2011
1 Enunciado
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ´esta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.
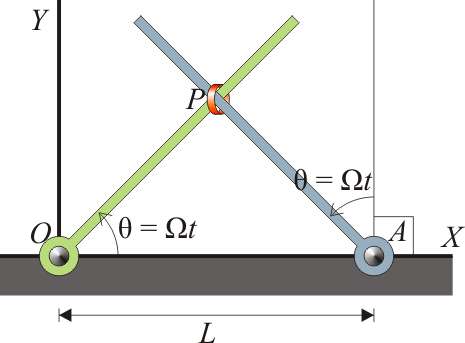
2 Sin considerar el peso
Conocemos el movimiento de la anilla: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular 2Ω y el radio de giro L / 2. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda,
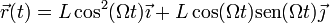
La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton