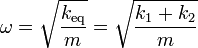Dos resortes enfrentados
De Laplace
| Línea 22: | Línea 22: | ||
Cuando <math>k_1\to\infty</math> las longitudes anteriores tienen el límite | Cuando <math>k_1\to\infty</math> las longitudes anteriores tienen el límite | ||
| - | <center><math>l_{1\,\mathrm{eq}\to l_{10} \qquad l_{2\mathrm{eq}}\to L - l_10</math></center> | + | <center><math>l_{1\,\mathrm{eq}}\to l_{10} \qquad l_{2\mathrm{eq}}\to L - l_10</math></center> |
que quiere decir que el muelle 1 se convierte en una barra rígida y no se estira en absoluto. Inversamente ocurre si <math>k_2\to\infty</math>. | que quiere decir que el muelle 1 se convierte en una barra rígida y no se estira en absoluto. Inversamente ocurre si <math>k_2\to\infty</math>. | ||
==Amplitud y frecuencia== | ==Amplitud y frecuencia== | ||
| + | Consideramos entonces las oscilaciones en torno a la posición de equilibrio. Estas vienen gobernadas por la ecuación de movimiento | ||
| + | |||
| + | <center><math>ma = -k_1(l_1-l_{10})+k_1(l_2-l_{20})\,</math></center> | ||
| + | |||
| + | junto con las condiciones iniciales | ||
| + | |||
| + | <center><math>l_{1}=l_{1\mathrm{eq}}\qquad\qquad l_{2}=l_{2\mathrm{eq}}\qquad v=v_0</math></center> | ||
| + | |||
| + | Si la masa se desvía una cantidad <math>x</math> las nuevas longitudes de los resortes son | ||
| + | |||
| + | <center><math>l_1=l_{1\mathrm{eq}}+x\qquad\qquad l_2=l_{2\mathrm{eq}}-x</math></center> | ||
| + | |||
| + | de forma que la ecuación de movimiento queda | ||
| + | |||
| + | <center><math>ma = -k_1x-k_2x-k_1(l_{1\mathrm{eq}}-l_{10}}+k_2(l_{2\mathrm{eq}}-l_{20}}</math></center> | ||
| + | |||
| + | Pero las longitudes de equilibrio son tales que se anulan los dos últimos términos y la ecuación se reduce a | ||
| + | |||
| + | <center><math>ma = -(k_1+k_2)x\,</math></center> | ||
| + | |||
| + | de donde llegamos a que la masa efectúa oscilaciones armónicas respecto a la posición de equilibrio, con la constante equivalente | ||
| + | |||
| + | <center><math>k_\mathrm{eq}=k_1+k_2</math></center> | ||
| + | |||
| + | La frecuencia angular de las oscilaciones resultantes vale | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{k_\mathrm{eq}}{m}}=\sqrt{\frac{k_1+k_2}{m}}</math></center> | ||
| + | |||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 23:35 25 nov 2011
1 Enunciado
Una partícula de masa m se encuentra situada entre dos resortes de longitudes en reposo l10 y l20, que se encuentran atados a paredes opuestas separadas una distancia L. Los muelles poseen constantes de recuperación k1 y k2.
- Determine la posición de equilibrio de la masa. ¿A cuanto tiende esta posición si
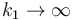? ¿Y si 
?
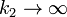- Estando en la posición de equilibrio, se le comunica a la masa una velocidad v0. Determine la amplitud y la frecuencia de las oscilaciones resultantes.
2 Posición de equilibrio
La posición de equilibrio es aquella en que la fuerza sobre la masa es nula. Esto ocurrirá cuando la fuerza con la que tira un muelle hacia uno de los lados es igual a la que ejercer el otro muelle hacia el lado opuesto. Si la masa se encuentra a una distancia l1 de la pared de la izquierda y a l2 de la de la derecha, la condición de equilibrio es
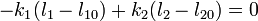
junto con la condición
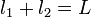
Despejando y sustituyendo queda
Cuando 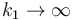las longitudes anteriores tienen el límite
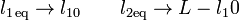
que quiere decir que el muelle 1 se convierte en una barra rígida y no se estira en absoluto. Inversamente ocurre si .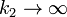
3 Amplitud y frecuencia
Consideramos entonces las oscilaciones en torno a la posición de equilibrio. Estas vienen gobernadas por la ecuación de movimiento
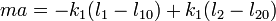
junto con las condiciones iniciales
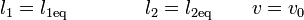
Si la masa se desvía una cantidad x las nuevas longitudes de los resortes son
de forma que la ecuación de movimiento queda
Pero las longitudes de equilibrio son tales que se anulan los dos últimos términos y la ecuación se reduce a
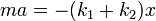
de donde llegamos a que la masa efectúa oscilaciones armónicas respecto a la posición de equilibrio, con la constante equivalente
La frecuencia angular de las oscilaciones resultantes vale
