Cuestión de cinemática, Noviembre 2011

De Laplace

(Diferencias entre revisiones)

Revisión de 18:01 24 nov 2011

Contenido

1 Enunciado
2 Solución
- 2.1 Ecuación paramétrica de la trayectoria
- 2.2 Ley horaria

1 Enunciado

El mecanismo de la figura consiste en un disco de radio

R

, siempre contenido en el plano vertical

O X Y

, que se mueve girando alrededor de un punto de su perímetro que coincide con el origen

O

del sistema de referencia. El movimiento del disco está descrito por la ley horaria

θ(t)

para el ángulo (medido en radianes) que forma el diámetro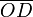 $\overline{OD}$ con la dirección horizontal

O X

. Se considera que el sistema parte de la posición inicial

θ = 0

. En el punto

D

hay conectada una cuerda flexible e inextensible de longitud

L = π R

que, cuando el disco gira, se va enrollando sobre su contorno, finalizando el proceso cuando

θ = π

. Además, un punto material pesado

P

hace que el tramo de cuerda no enrollado siempre penda verticalmente.

Obtenga la ecuación paramétrica de la trayectoria $Γ$ .
El extremo $D$ del diámetro realiza un movimiento circular uniforme, siendo su aceleración 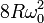$8R\omega_0^2$ . ¿Cómo es la correspondiente ley horaria para el ángulo $θ$ ?
Calcule la expresión de la componente intrínseca de la velocidad de la partícula $P$ .
Aceleración tangencial del punto $P$ .
Radio de curvatura de la trayectoria de $P$ en el punto de inicial.

2 Solución

2.1 Ecuación paramétrica de la trayectoria

Obtendremos la ecuación paramétrica de la trayectoria $Γ$ seguida por el punto $P$ , en términos de la variable geométrica que describe el movimiento de rotación del disco alrededor del punto $O$ : el ángulo $θ$ . Para ello, descompondremos el radiovector que indica la posición de $P$ respecto de $O$ , en la suma de varios segmentos orientados de descripción sencilla:

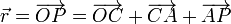
$\vec{r}=\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CA}+\overrightarrow{AP}$

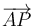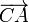El segmento orientado $\overrightarrow{AP}$ coincide con el tramo de cuerda desenrollada que pende verticalmente. En el sistema de referencia adoptado, la dirección vertical está indicada por el unitario $\vec{\jmath}$ . Por otra parte, este segmento es tangente al disco en el punto $A$ y, por tanto, perpendicular a la dirección radial $\overrightarrow{CA}$ que, en consecuencia, es horizontal y paralela a la $\vec{\imath}$ . Finalmente, el segmento $\overrightarrow{OC}$ es un radio del disco y forma un ángulo $θ$ con la dirección horizontal $O X$ . Se tendrá, por tanto:

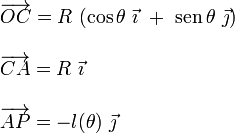
$\begin{array}{l}\displaystyle\overrightarrow{OC}=R\ (\cos\theta\ \vec{\imath}\ +\ \mathrm{sen}\!\ \theta\ \vec{\jmath})\\ \\ \overrightarrow{CA}=R\ \vec{\imath}\\ \\ \overrightarrow{AP}=- l(\theta)\ \vec{\jmath}\end{array}$

donde $l (θ)$ es la longitud del tramo de cuerda desenrollado que, obviamente, dependerá de la posición del disco (y, por tanto, del ángulo $θ$ ). Concretamente, esta longitud será igual a la longitud total de la cuerda menos la del trozo enrollado en el arco de circunferencia comprendido entre los puntos $D$ y $A$ . Obsérvese que el ángulo 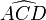$\widehat{ACD}$ que abarca a dicho arco es también $θ$ , por lo que:

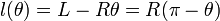
$\displaystyle l(\theta)=L-R\theta=R(\pi-\theta)$

Podemos obtener así la expresión paramétrica de la curva $Γ$ en términos del ángulo $θ$ :

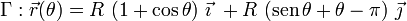
$\overrightarrow{OP}=R\ (\cos\theta\ \vec{\imath} + \mathrm{sen}\!\ \theta \vec{\jmath}\ )+ R\ [\ \vec{\imath} - l(\theta)\ \vec{\jmath}\ ]$ $\Rightarrow$ $\Gamma:\vec{r}(\theta)=R\ (1+\cos\theta )\ \vec{\imath}\ + R\ ( \mathrm{sen}\!\ \theta + \theta - \pi )\ \vec{\jmath}$

2.2 Ley horaria

Para completar la descripción del movimiento de la partícula $P$ hemos de determinar la ley horaria. Y puesto que la trayectoria se ha descrito en términos del ángulo $θ$ que forma el diámetro 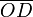$\overline{OD}$ del disco con la horizontal $O X$ , lo más inmediato es obtener la ley horaria $θ(t)$ correspondiente a dicho parámetro geométrico. Para ello, utilizaremos la información dada en el enunciado de que, cuando el sistema se mueve de manera que el disco gira en el plano $O X Y$ manteniéndose fijo el punto $O$ , el punto del disco diametralmente opuesto, $D$ , realiza un movimiento circular uniforme cuya aceleración tiene un valor conocido. Además, obsérvese que la trayectoria de dicho movimiento va a ser una circunferencia (obviamente contenida en el plano $O X Y$ , con centro en $O$ y ¡radio $2 R$ ! Por tanto, las ecuaciones de movimiento para dicho punto son:

$\overrightarrow{OD}=\vec{r}_D(t)=2R\big[\cos\theta (t) \vec{\imath}+\mathrm{sen}\!\ \theta(t)\vec{\jmath}\bigg]$

Es decir, la ley horaria de este movimiento circular va a ser, precisamente, la que utilizaremos para describir el movimiento de la partícula $P$ .

\smallskip

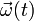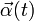Como sabemos, si el punto $D$ realiza un movimiento circular, su valocidad y aceleración pueden expresarse en términos del radio-vector posición y de sendos vectores, $\vec{\omega}(t)$ (vector rotación instantánea), y $\vec{\alpha}(t)$ (su derivada temporal), perpendiculares al plano del movimiento y, en general, variables en el tiempo:

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \begin{array}{l}\displaystyle

ede expresarse

@@ Línea 34: / Línea 34: @@
 Para completar la descripción del movimiento de la partícula <math>P</math> hemos de determinar la ley horaria. Y puesto que la trayectoria se ha descrito en términos del ángulo <math>\theta</math> que forma el diámetro <math>\overline{OD}</math> del disco con la horizontal <math>OX</math>, lo más inmediato es obtener la ley horaria <math>\theta(t)</math> correspondiente a dicho parámetro geométrico. Para ello, utilizaremos la información dada en el enunciado de que, cuando el sistema se mueve de manera que el disco gira en el plano <math>OXY</math> manteniéndose fijo el punto <math>O</math>, el punto del disco diametralmente opuesto, <math>D</math>, realiza un movimiento circular uniforme cuya aceleración tiene un valor conocido. Además, obsérvese que la trayectoria de dicho movimiento va a ser una circunferencia (obviamente contenida en el plano <math>OXY</math>, con centro en <math>O</math> y ¡radio <math>2R</math>! Por tanto, las ecuaciones de movimiento para dicho punto son:
-<center><math>\overrightarrow{OD}=\vec{r}_D(t)=2R\big[\cos\theta (t) \vec{\imath}+\mathrm{sen}\!\ \theta(t)\vec{jmath}\bigg]</math></center>
+<center><math>\overrightarrow{OD}=\vec{r}_D(t)=2R\big[\cos\theta (t) \vec{\imath}+\mathrm{sen}\!\ \theta(t)\vec{\jmath}\bigg]</math></center>
+Es decir, la ley horaria de este movimiento circular va a ser, precisamente, la que utilizaremos para describir el movimiento de la partícula <math>P</math>.
+\smallskip
+Como sabemos, si el punto <math>D</math> realiza un movimiento circular,
+su valocidad y aceleración pueden expresarse en términos del radio-vector posición y de sendos vectores, <math>\vec{\omega}(t)</math>(vector rotación instantánea), y <math>\vec{\alpha}(t)</math> (su derivada temporal), perpendiculares al plano del movimiento y, en general, variables en el tiempo:
+<center><math>\begin{array}{l}\displaystyle</math></center>
+ede expresarse

Cuestión de cinemática, Noviembre 2011

De Laplace

Revisión de 18:01 24 nov 2011

Contenido

1 Enunciado

2 Solución

2.1 Ecuación paramétrica de la trayectoria

2.2 Ley horaria

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES