2.5. Rectilíneo con desaceleración creciente (Ex.Nov/11)
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula <math>\,\vec{a}(t)=-Kt\,\vec{\imath}\,\,</math>, donde <math>K\,</math> es una constante de valor igual a 8.00 m/s<math>^{3}</math>. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá? | Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula <math>\,\vec{a}(t)=-Kt\,\vec{\imath}\,\,</math>, donde <math>K\,</math> es una constante de valor igual a 8.00 m/s<math>^{3}</math>. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá? | ||
| + | |||
| + | ==Velocidad y posición== | ||
| + | Se trata de un movimiento rectilíneo a lo largo del eje OX. Por tanto, podemos escribir: | ||
| + | |||
| + | <center><math>\vec{r}=x\,\vec{\imath}\,\,;\,\,\,\,\,\, \vec{v}=v_x\,\vec{\imath}=\dot{x}\,\vec{\imath}\,\,;\,\,\,\,\,\, \vec{a}=a_x\,\vec{\imath}=\dot{v_x}\,\vec{\imath}=\ddot{x}\,\vec{\imath}=-Kt\,\vec{\imath}\,\,\,\mbox{para t>0)}</math></center> | ||
| + | |||
| + | Considerando por simplicidad que el origen de coordenadas coincide con la posición de la partícula en el instante en que se detecta el obstáculo (t=0), conocemos también las condiciones iniciales: | ||
| + | |||
| + | <center><math>x(0)=0\,\,;\,\,\,\,\,\,\,\,\,\, v_x(0)=\dot{x}(0)=25\,\mathrm{m}/\mathrm{s}</math></center> | ||
| + | |||
| + | Por tanto, determinar la velocidad y la posición de la partícula para t>0 se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico: | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}v_x}{\mathrm{d}t}=-Kt\,\,\,\,\,\longroghtarrow\,\,\,\,\,\mathrm{d}v_x=-Kt\mathrm{d}t\,\,\,\,\,\longroghtarrow\,\,\,\,\,\int_{v_x(0)}^{v_x(t)}\!\mathrm{d}v_x=-K\int_{0}^{t}\!t\mathrm{d}t\,\,\,\,\,\longroghtarrow\,\,\,\,\,v_x(t)=v_x(0)-\frac{1}{2}Kt^2 </math></center> | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}x}{\mathrm{d}t}=v_x(0)-\frac{1}{2}Kt^2\,\,\,\,\,\longroghtarrow\,\,\,\,\,\mathrm{d}x=\left(v_x(0)-\frac{1}{2}Kt^2\right)\mathrm{d}t\,\,\,\,\,\longroghtarrow\,\,\,\,\,\int_{x(0)}^{x(t)}\!\mathrm{d}x=\int_{0}^{t}\!\left(v_x(0)-\frac{1}{2}Kt^2\right)\mathrm{d}t\,\,\,\,\,\longroghtarrow\,\,\,\,\,x(t)=x(0)+v_x(0)t-\frac{1}{6}Kt^3</math></center> | ||
| + | |||
| + | ==Tiempo que tarda en detenerse== | ||
| + | La partícula se detendrá en el instante <math>t=t^*\,</math> en el que se anule su velocidad, es decir: | ||
| + | |||
| + | <center><math>v_x(t*)=0\,\,\,\,\,\longroghtarrow\,\,\,\,\,v_x(0)-\frac{1}{2}K(t^*)^2=0\,\,\,\,\,\longroghtarrow\,\,\,\,\,t^*=\sqrt{\frac{2v_x(0)}{K}}</math></center> | ||
| + | |||
| + | y sustituyendo los datos numéricos: | ||
| + | |||
| + | <center><math>t^*=\sqrt{\frac{2\cdot 25\,\mathrm{m}/\mathrm{s}}{8\,\mathrm{m}/\mathrm{s}^3}}\,\mathrm{s}=2.50\,\mathrm{s}</math></center> | ||
| + | |||
| + | ==Distancia del obstáculo a la que se detiene== | ||
| + | Se trata simplemente de evaluar la posición (coordenada <math>x\,</math>) de la partícula para el instante en que se detiene, y después restarle el valor de esa posición de la partícula a la posición en la que se encuentra el obstáculo: | ||
| + | |||
| + | <center><math>d=x_{\mathrm{obs}}-x(t^*)=x_{\mathrm{obs}}-\left(x(0)+v_x(0)t^*-\frac{1}{6}K(t^*)^3\right)=x_{\mathrm{obs}}-x(0)-v_x(0)t^*+\frac{1}{6}K(t^*)^3</math></center> | ||
| + | |||
| + | y sustituyendo los datos numéricos: | ||
| + | |||
| + | <center><math>d=50\,\mathrm{m}-0\,\mathrm{m}-25\,\mathrm{m}/\mathrm{s}\cdot 2.50\,\mathrm{s}+\frac{1}{6}8\,\mathrm{m}/\mathrm{s}^3}\cdot(2.50\,\mathrm{s})^3=8.33\,\mathrm{m}</math></center> | ||
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
Revisión de 18:36 12 nov 2011
Contenido |
1 Enunciado
Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula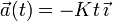 
, donde 
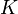es una constante de valor igual a 8.00 m/s3. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá?
2 Velocidad y posición
Se trata de un movimiento rectilíneo a lo largo del eje OX. Por tanto, podemos escribir:
Considerando por simplicidad que el origen de coordenadas coincide con la posición de la partícula en el instante en que se detecta el obstáculo (t=0), conocemos también las condiciones iniciales:
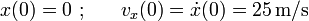
Por tanto, determinar la velocidad y la posición de la partícula para t>0 se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:
3 Tiempo que tarda en detenerse
La partícula se detendrá en el instante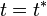 
en el que se anule su velocidad, es decir:
y sustituyendo los datos numéricos:
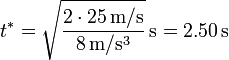
4 Distancia del obstáculo a la que se detiene
Se trata simplemente de evaluar la posición (coordenada 
) de la partícula para el instante en que se detiene, y después restarle el valor de esa posición de la partícula a la posición en la que se encuentra el obstáculo:
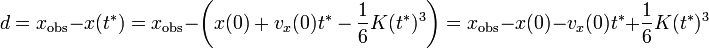
y sustituyendo los datos numéricos:
