3.12. Equilibrio de partícula en hélice
De Laplace
(→Equilibrio) |
(→Equilibrio) |
||
| Línea 8: | Línea 8: | ||
==Equilibrio== | ==Equilibrio== | ||
La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle | La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle | ||
| - | y la fuerza de reacción vincular | + | y la fuerza de reacción vincular, las cuales se pueden expresar en la base cartesiana ortonormal como: |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<center><math>\begin{array}{rcl} m\vec{g} & = & -mg\vec{k} \\ | <center><math>\begin{array}{rcl} m\vec{g} & = & -mg\vec{k} \\ | ||
| Línea 20: | Línea 16: | ||
</math></center> | </math></center> | ||
| - | + | Obsérvese que, al evaluar la fuerza elástica ejercida por el resorte, se ha tenido en cuenta la ecuación del vínculo (hélice), ya que ésta define las únicas posiciones posibles de la partícula: | |
<center><math>\vec{r} = A\,\mathrm{cos}(\theta)\,\vec{\imath}+A\,\mathrm{sen}(\theta)\,\vec{\jmath}+\frac{b\theta}{2\pi}\,\vec{k}</math></center> | <center><math>\vec{r} = A\,\mathrm{cos}(\theta)\,\vec{\imath}+A\,\mathrm{sen}(\theta)\,\vec{\jmath}+\frac{b\theta}{2\pi}\,\vec{k}</math></center> | ||
| + | |||
| + | En el equilibrio, la resultante de las tres fuerzas debe ser nula | ||
| + | |||
| + | <center><math>m\vec{g}-k\vec{r}+\vec{\Phi}=\vec{0}</math></center> | ||
| + | |||
| + | Igualando, componente a componente, esta ecuación vectorial da lugar a tres ecuaciones escalares: | ||
| + | |||
| + | <center><math>\begin{array}{rcl} -kA\,\mathrm{cos}(\theta)+\Phi_x & = & 0 \,\, (1)\\ -kA\,\mathrm{sen}(\theta)+\Phi_y & = & 0 \,\, (2)\\ -mg-kb\,\theta/(2\pi)+\Phi_z & = & 0 \,\, (3) | ||
| + | \end{array} | ||
| + | </math></center> | ||
Por otra parte, la fuerza de reacción vincular tiene necesariamente dirección perpendicular a la hélice (pues no se menciona que exista rozamiento, es decir, se sobreentiende que la hélice es un vínculo liso). Un vector tangente a la hélice es | Por otra parte, la fuerza de reacción vincular tiene necesariamente dirección perpendicular a la hélice (pues no se menciona que exista rozamiento, es decir, se sobreentiende que la hélice es un vínculo liso). Un vector tangente a la hélice es | ||
| Línea 28: | Línea 34: | ||
<center><math>\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta} = -A\,\mathrm{sen}(\theta)\,\vec{\imath}+A\,\mathrm{cos}(\theta)\,\vec{\jmath}+\frac{b}{2\pi}\,\vec{k}</math></center> | <center><math>\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta} = -A\,\mathrm{sen}(\theta)\,\vec{\imath}+A\,\mathrm{cos}(\theta)\,\vec{\jmath}+\frac{b}{2\pi}\,\vec{k}</math></center> | ||
| - | Por tanto, podemos | + | Por tanto, podemos garantizar que <math>\vec{\Phi}</math> será ortogonal a la hélice exigiendo la nulidad del siguiente producto escalar |
| + | |||
| + | <center><math>\vec{\Phi}\cdot\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta} = 0 \Longrightarrow -A\,\mathrm{sen}(\theta)\Phi_x+A\,\mathrm{cos}(\theta)\Phi_y+\frac{b}{2\pi}\Phi_z=0\,\, (4)</math></center> | ||
| - | + | Hemos obtenido en definitiva un sistema de cuatro ecuaciones (1-4) con cuatro incógnitas, que son los valores de <math>\theta\,</math>, <math>\Phi_x\,</math>, <math>\Phi_y\,</math> y <math>\Phi_z\,</math> correspondientes a la posición de equilibrio. | |
==Fuerza de reacción vincular== | ==Fuerza de reacción vincular== | ||
Revisión de 14:01 26 oct 2011
Contenido |
1 Enunciado
Una partícula de masa m se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante k y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada en la hélice de ecuaciones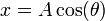 
, 
, 
.
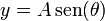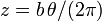- Determine la posición de equilibrio de la partícula sobre la hélice.
- Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio.
- Determine la energía potencial como función del parámetro
y discuta la estabilidad de la posición de equilibrio.
2 Equilibrio
La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle y la fuerza de reacción vincular, las cuales se pueden expresar en la base cartesiana ortonormal como:
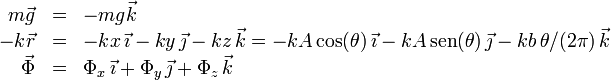
Obsérvese que, al evaluar la fuerza elástica ejercida por el resorte, se ha tenido en cuenta la ecuación del vínculo (hélice), ya que ésta define las únicas posiciones posibles de la partícula:
En el equilibrio, la resultante de las tres fuerzas debe ser nula
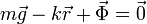
Igualando, componente a componente, esta ecuación vectorial da lugar a tres ecuaciones escalares:
Por otra parte, la fuerza de reacción vincular tiene necesariamente dirección perpendicular a la hélice (pues no se menciona que exista rozamiento, es decir, se sobreentiende que la hélice es un vínculo liso). Un vector tangente a la hélice es
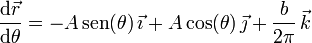
Por tanto, podemos garantizar que 
será ortogonal a la hélice exigiendo la nulidad del siguiente producto escalar
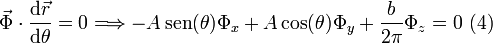
Hemos obtenido en definitiva un sistema de cuatro ecuaciones (1-4) con cuatro incógnitas, que son los valores de , 
, 
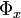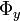y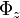 
correspondientes a la posición de equilibrio.
