Movimiento en un tiro parabólico
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 14: | Línea 14: | ||
| - | <center>[[Archivo:angry-bird-parabola.png|angry-bird-parabola.png]]</center> | + | <center>[[Archivo:angry-bird-parabola.png|angry-bird-parabola.png|400px]]</center> |
==Posición, velocidad y aceleración== | ==Posición, velocidad y aceleración== | ||
Revisión de 15:57 13 oct 2011
Contenido |
1 Enunciado
Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante
una posición inicial nula (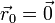
) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.
- Determine el vector de posición, la velocidad y la aceleración en cada instante.
- Halle el punto donde la partícula impacta con el suelo. ¿Cuál es el alcance máximo para una rapidez inicial dada?
- Calcule la celeridad y el vector tangente en el instante inicial y en el instante en que se encuentra a mayor altura.
- Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los dos instantes anteriores.
- Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
- Suponga que se quiere alcanzar un blanco situado a 60 m con un mortero que comunica una rapidez inicial de 25 m/s. ¿Con qué ángulo debe dispararse si en medio se encuentra un eucalipto de 15 m de altura? (supóngase
)
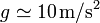