Entrar Página Discusión Historial Go to the site toolbox

Cálculo numérico de la derivada del seno

De Laplace

(Diferencias entre revisiones)
(→Aproximación numérica)
Línea 30: Línea 30:
! <math>x^\circ</math>
! <math>x^\circ</math>
! <math>\mathrm{sen}(x^\circ)</math>
! <math>\mathrm{sen}(x^\circ)</math>
-
! <math>\mathrm{sen}(x^\circ)/\Delta x</math>
+
! <math>\mathrm{sen}(x^\circ)/x^\circ</math>
|-
|-
| 1
| 1
Línea 60: Línea 60:
| 0.017453292519943294883
| 0.017453292519943294883
|}
|}
 +
 +
Vemos que efectivamente el cociente converge, pero desde luego no a 1, que es lo que cabría esperar (si la derivada del seno es el coseno, al hacer <math>x=0</math>, nos debería salir 1).
 +
 +
==Interpretación del resultado==
 +
Para interpretar el resultado, seguimos la sugerencia del enunciado y multiplicamos el resultado por 180, a ver qué sale
 +
 +
{| class="bordeado"
 +
|-
 +
! <math>x^\circ</math>
 +
! <math>\mathrm{sen}(x^\circ)</math>
 +
! <math>\mathrm{sen}(x^\circ)/x^\circ</math>
 +
| <math>180 \mathrm{sen}(x^\circ)/x^\circ</math>
 +
|-
 +
| 1
 +
| 0.017452406437283512819
 +
| 0.017452406437283512819
 +
| 3.1414331587110323075
 +
|-
 +
| 0.1
 +
| 0.001745328365898308836
 +
| 0.017453283658983088358
 +
| 3.1415910586169559044
 +
|-
 +
| 0.01
 +
| 0.001745329243133368033
 +
| 0.017453292431333680334
 +
| 3.1415926376400624601
 +
|-
 +
| 0.001
 +
| 0.000174532925190571996
 +
| 0.017453292519057199614
 +
| 3.1415926534302959304
 +
|-
 +
| 0.0001
 +
| 0.000017453292519934435
 +
| 0.017453292519934434808
 +
| 3.1415926535881982654
 +
|-
 +
| 0.00001
 +
| 0.000001745329251994321
 +
| 0.017453292519943207160
 +
| 3.1415926535897772887
 +
|-
 +
| 0.000001
 +
| 0.000000174532925199433
 +
| 0.017453292519943294883
 +
| 3.1415926535897930790
 +
|-
 +
| ···
 +
| ···
 +
| ···
 +
| ···
 +
|-
 +
| 0
 +
| 0
 +
| &pi;/180
 +
| &pi;
 +
|}
 +
[[Categoría:Problemas de herramientas matemáticas (GIE)]]
[[Categoría:Problemas de herramientas matemáticas (GIE)]]

Revisión de 22:06 5 oct 2011

Contenido

1 Enunciado

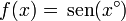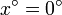Se trata de calcular la derivada de f(x)=\,\mathrm{sen}(x^\circ) para x^\circ=0^\circ.

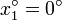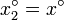  1. Exprese el cociente Δf / Δx, cuando x_1^\circ=0^\circ y x_2^\circ=x^\circ.
  2. Calcule numéricamente el cociente anterior para 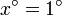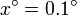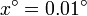x^\circ=1^\circ, x^\circ=0.1^\circ, x^\circ=0.01^\circ,… hasta 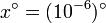x^\circ=(10^{-6})^\circ. ¿A cuanto tiende el límite?
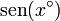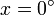  3. Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de \mathrm{sen}(x^\circ) en x=0^\circ?

2 Cociente incremental

La derivada de una función equivale al límite del cociente entre incrementos cuando estos tienden a cero

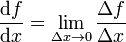
\frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x}

En nuestro caso, consideramos un incremento entre 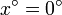x^\circ = 0^\circ y un cierto valor del ángulo

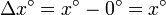
\Delta x^\circ = x^\circ - 0^\circ = x^\circ

mientras que el incremento en la función es

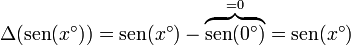
\Delta(\mathrm{sen}(x^\circ))=\mathrm{sen}(x^\circ)-\overbrace{\mathrm{sen}(0^\circ)}^{=0}= \mathrm{sen}(x^\circ)

Por tanto, el cociente entre incrementos se reduce a

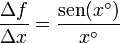
\frac{\Delta f}{\Delta x}=\frac{\mathrm{sen}(x^\circ)}{x^\circ}

3 Aproximación numérica

Calculamos entonces los valores del cociente incremental para valores cada vez más pequeños del argumento

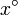
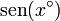
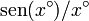
x^\circ \mathrm{sen}(x^\circ) \mathrm{sen}(x^\circ)/x^\circ
1 0.017452406437283512819 0.017452406437283512819
0.1 0.001745328365898308836 0.017453283658983088358
0.01 0.001745329243133368033 0.017453292431333680334
0.001 0.000174532925190571996 0.017453292519057199614
0.0001 0.000017453292519934435 0.017453292519934434808
0.00001 0.000001745329251994321 0.017453292519943207160
0.000001 0.000000174532925199433 0.017453292519943294883

Vemos que efectivamente el cociente converge, pero desde luego no a 1, que es lo que cabría esperar (si la derivada del seno es el coseno, al hacer x = 0, nos debería salir 1).

4 Interpretación del resultado

Para interpretar el resultado, seguimos la sugerencia del enunciado y multiplicamos el resultado por 180, a ver qué sale

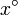
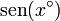
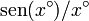
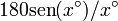
x^\circ \mathrm{sen}(x^\circ) \mathrm{sen}(x^\circ)/x^\circ 180 \mathrm{sen}(x^\circ)/x^\circ
1 0.017452406437283512819 0.017452406437283512819 3.1414331587110323075
0.1 0.001745328365898308836 0.017453283658983088358 3.1415910586169559044
0.01 0.001745329243133368033 0.017453292431333680334 3.1415926376400624601
0.001 0.000174532925190571996 0.017453292519057199614 3.1415926534302959304
0.0001 0.000017453292519934435 0.017453292519934434808 3.1415926535881982654
0.00001 0.000001745329251994321 0.017453292519943207160 3.1415926535897772887
0.000001 0.000000174532925199433 0.017453292519943294883 3.1415926535897930790
··· ··· ··· ···
0 0 π/180 π
Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_num%C3%A9rico_de_la_derivada_del_seno"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace