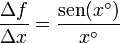Cálculo numérico de la derivada del seno
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se trata de calcular la derivada de <math>f(x)=\,\mathrm{sen}(x^\circ)</math> para <math>x^\circ=0^\circ</math>. # Exprese el cociente <math>\Delta f/\Delta x</ma…') |
|||
| Línea 6: | Línea 6: | ||
# Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de <math>\mathrm{sen}(x^\circ)</math> en <math>x=0^\circ</math>? | # Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de <math>\mathrm{sen}(x^\circ)</math> en <math>x=0^\circ</math>? | ||
| + | ==Cociente incremental== | ||
| + | La derivada de una función equivale al límite del cociente entre incrementos cuando estos tienden a cero | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x}</math></center> | ||
| + | |||
| + | En nuestro caso, consideramos un incremento entre <math>x^\circ = 0^\circ</math> y un cierto valor del ángulo | ||
| + | |||
| + | <center><math>\Delta x^\circ = x^\circ - 0^\circ = x^\circ</math></center> | ||
| + | |||
| + | mientras que el incremento en la función es | ||
| + | |||
| + | <center><math>\Delta(\mathrm{sen}(x^\circ))=\mathrm{sen}(x^\circ)-\overbrace{\mathrm{sen}(0^\circ)}^{=0}= \mathrm{sen}(x^\circ)</math></center> | ||
| + | |||
| + | Por tanto, el cociente entre incrementos se reduce a | ||
| + | |||
| + | <center><math>\frac{\Delta f}{\Delta x}=\frac{\mathrm{sen}(x^\circ)}{x^\circ}</math></center> | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 21:50 5 oct 2011
1 Enunciado
Se trata de calcular la derivada de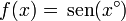 
para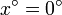 
.
- Exprese el cociente Δf / Δx, cuando
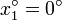y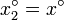 
.
- Calcule numéricamente el cociente anterior para
, 
, 
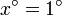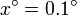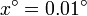,… hasta 
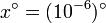. ¿A cuanto tiende el límite?
- Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de
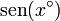en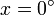 
?
2 Cociente incremental
La derivada de una función equivale al límite del cociente entre incrementos cuando estos tienden a cero
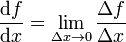
En nuestro caso, consideramos un incremento entre 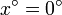y un cierto valor del ángulo
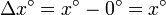
mientras que el incremento en la función es
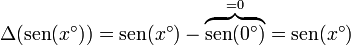
Por tanto, el cociente entre incrementos se reduce a
