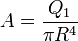Distribución de carga dentro de esferas conductoras
De Laplace
(Diferencias entre revisiones)
(→Cálculo de la constante A) |
(→Cálculo de la constante A) |
||
| Línea 10: | Línea 10: | ||
El valor de la constante $A$ lo obtenemos del valor de la carga total, que es conocida. Esta carga debe ser igual a la integral de la densidad <math>\rho</math> | El valor de la constante $A$ lo obtenemos del valor de la carga total, que es conocida. Esta carga debe ser igual a la integral de la densidad <math>\rho</math> | ||
| - | <math>Q_1= \int \rho\,\mathrm{d}\tau = \int_0^{2\pi}\!\! \!\! \mathrm{d}\varphi\int_0^\pi\!\!\mathrm{d}\theta\,\mathrm{sen}\,\theta\int_0^R \!\! dr\,r^2(A r) = 4\pi A\frac{R^4}{4}= \pi A R^4</math> | + | <center><math>Q_1= \int \rho\,\mathrm{d}\tau = \int_0^{2\pi}\!\! \!\! \mathrm{d}\varphi\int_0^\pi\!\!\mathrm{d}\theta\,\mathrm{sen}\,\theta\int_0^R \!\! dr\,r^2(A r) = 4\pi A\frac{R^4}{4}= \pi A R^4</math></center> |
y de aquí | y de aquí | ||
Revisión de 16:05 3 jul 2008
Contenido |
1 Enunciado
Una esfera de radio R posee una carga Q1 distribuida en su volumen de modo que la densidad volumétrica es ρ(r) = Ar. A su alrededor se disponen dos superficies esféricas metálicas concéntricas, de radios 2R y 4R, respectivamente. Estas esferas están aisladas y descargadas.
- Calcule la constante A en función de la carga de la esfera y de su radio.
- Calcule el campo eléctrico en todo el espacio y el potencial al que se encuentran las esferas conductoras.
- Se conectan las dos esferas conductoras entre sí. ¿Cuál es el nuevo potencial y la nueva carga de cada esfera?
2 Solución
2.1 Cálculo de la constante A
El valor de la constante $A$ lo obtenemos del valor de la carga total, que es conocida. Esta carga debe ser igual a la integral de la densidad ρ
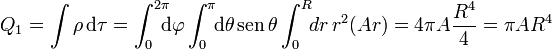
y de aquí