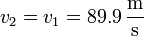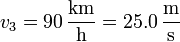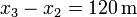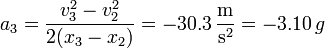Entrar Página Discusión Historial Go to the site toolbox

Aceleración en un tramo rectilíneo (GIE)

De Laplace

(Diferencias entre revisiones)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
La longitud de la recta principal del circuito de Monza mide 1.3 km. Un Ferrari entra en la recta a 260km/h y acelera durante 0.8 km hasta alcanzar 340&thinsP,km/h. Mantiene esta velocidad hasta estar a 150 m de la primera chicane, a la que llega a 80 km/h. Un Red Bull entra en la misma recta a 280 km/h, acelera hasta 320 km/h durante 0.7 km y frena al llegar a 120 m de la chicane, en la que entra a 90 km/h.
+
La longitud de la recta principal del circuito de Monza mide 1.3 km. Un Ferrari entra en la recta a 260km/h y acelera durante 0.8 km hasta alcanzar 340&thinsP,km/h. Mantiene esta velocidad hasta estar a 150 m de la primera ''chicane'', a la que llega a 80 km/h. Un Red Bull entra en la misma recta a 280 km/h, acelera hasta 320 km/h durante 0.7 km y frena al llegar a 120 m de la ''chicane'', en la que entra a 90 km/h.
Suponiendo que las aceleraciones son constantes en cada uno de los tramos
Suponiendo que las aceleraciones son constantes en cada uno de los tramos
Línea 22: Línea 22:
v & = & v_0 + a t \\
v & = & v_0 + a t \\
\end{array}</math></center>
\end{array}</math></center>
 +
 +
Si elevamos al cuadrado la segunda nos queda
 +
 +
<center><math>v^2 = v_0^2 + 2v_0at + a^2 t^2 = v_0^2 + 2a\left(v_0t + \frac{1}{2}at^2\right)= v_0^2+2a(x-x_0)</math></center>
 +
 +
Despejando de aquí
 +
 +
<center><math>a = \frac{v^2-v_0^2}{2(x-x_0)}</math></center>
 +
 +
Llevando esto al límite obtenemos la relación general
 +
 +
<center><math>a = \frac{1}{2}\frac{\mathrm{d}\ }{\mathrm{d}x}(v^2)</math></center>
 +
 +
esto es, en un movimiento uniformemente acelerado se obtiene una recta en la gráfica de <math>v^2</math> frente a <math>x</math>, no en la de <math>v(x)</math>.
 +
 +
Podemos aplicar esta fórmula a los diferentes casos indicados en el enunciado:
 +
 +
;Ferrari: En el primer tramo tenemos
 +
 +
<center><math>v_0 = 260\,\frac{\mathrm{km}}{\mathrm{h}} = 72.2\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>v_1 = 340\,\frac{\mathrm{km}}{\mathrm{h}} = 94.4\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>x_1-x_0 = 800\,\mathrm{m}</math></center>
 +
 +
:lo que nos da la aceleración
 +
 +
<center><math>a_1 = \frac{v_1^2-v_0^2}{2(x_1-x_0)}=2.31\,\frac{\mathrm{m}}{\mathrm{s}^2} = 0.24\,g</math></center>
 +
 +
:En el segundo tramo, en que el movimiento es uniforme, la aceleración es nula.
 +
 +
<center><math>a_2 = 0.00\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
 +
 +
:En el tercer tramo operamos del mismo modo
 +
 +
<center><math>v_2 = v_1 = 94.4\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>v_3 = 80\,\frac{\mathrm{km}}{\mathrm{h}} = 22.2\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>x_3-x_2 = 150\,\mathrm{m}</math></center>
 +
 +
:y nos queda la aceleración
 +
 +
<center><math>a_3 = \frac{v_3^2-v_2^2}{2(x_3-x_2)}= -28.1\,\frac{\mathrm{m}}{\mathrm{s}^2} = -2.86\,g</math></center>
 +
 +
:Vemos que la aceleración es mucho más intensa en la frenada que en el tramo acelerado.
 +
 +
 +
;Red Bull: Operando igualmente, en el primer tramo tenemos
 +
 +
<center><math>v_0 = 280\,\frac{\mathrm{km}}{\mathrm{h}} = 77.8\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>v_1 = 320\,\frac{\mathrm{km}}{\mathrm{h}} = 88.9\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>x_1-x_0 = 700\,\mathrm{m}</math></center>
 +
 +
:y queda la aceleración
 +
 +
<center><math>a_1 = \frac{v_1^2-v_0^2}{2(x_1-x_0)}=1.32\,\frac{\mathrm{m}}{\mathrm{s}^2} = 0.13\,g</math></center>
 +
 +
:En el segundo tramo la aceleración es nula.
 +
 +
<center><math>a_2 = 0.00\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
 +
 +
:y en el tercer tramo vale
 +
 +
<center><math>v_2 = v_1 = 89.9\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>v_3 = 90\,\frac{\mathrm{km}}{\mathrm{h}} = 25.0\,\frac{\mathrm{m}}{\mathrm{s}}</math>{{qquad}}{{qquad}}<math>x_3-x_2 = 120\,\mathrm{m}</math></center>
 +
 +
<center><math>a_3 = \frac{v_3^2-v_2^2}{2(x_3-x_2)}= -30.3\,\frac{\mathrm{m}}{\mathrm{s}^2} = -3.10\,g</math></center>
 +
 +
==Velocidad media==
 +
 +
[[Categoría:Cinemática de la partícula (GIE)]]
[[Categoría:Cinemática de la partícula (GIE)]]

Revisión de 20:56 19 sep 2011

1 Enunciado

La longitud de la recta principal del circuito de Monza mide 1.3 km. Un Ferrari entra en la recta a 260km/h y acelera durante 0.8 km hasta alcanzar 340&thinsP,km/h. Mantiene esta velocidad hasta estar a 150 m de la primera chicane, a la que llega a 80 km/h. Un Red Bull entra en la misma recta a 280 km/h, acelera hasta 320 km/h durante 0.7 km y frena al llegar a 120 m de la chicane, en la que entra a 90 km/h.

Suponiendo que las aceleraciones son constantes en cada uno de los tramos

  1. Determine las aceleraciones de los dos vehículos en cada uno de los tramos. Exprese el resultado como múltiplo de g.
  2. Calcule la velocidad media de cada uno. ¿Cuál tarda menos en hacer en recorrer la recta?
  3. Represente las gráficas de velocidad frente a la posición y frente al tiempo.

2 Aceleraciones

A la vista de este problema, la tentación es pensar que la gráfica de la velocidad de uno de los coches respecto a la posición tiene una gráfica del estilo de la siguiente:

y que la aceleración es la pendiente de cada tramo. Esto es doblemente incorrecto:

  • La aceleración es la derivada de la velocidad respecto al tiempo, no respecto a la posición.
  • No sabemos todavía como depende la velocidad de la posición. Aceleración constante no quiere decir que la gráfica v(x) sea una recta (no lo es).

Para obtener la aceleración en un movimiento uniformemente acelerado, aplicamos las dos relaciones

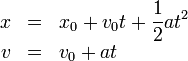
\begin{array}{rcl} x & = & \displaystyle x_0 + v_0 t + \frac{1}{2}a t^2 \\ v & = & v_0 + a t \\ \end{array}

Si elevamos al cuadrado la segunda nos queda

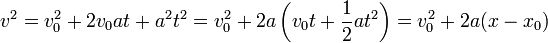
v^2 = v_0^2 + 2v_0at + a^2 t^2 = v_0^2 + 2a\left(v_0t + \frac{1}{2}at^2\right)= v_0^2+2a(x-x_0)

Despejando de aquí

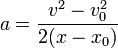
a = \frac{v^2-v_0^2}{2(x-x_0)}

Llevando esto al límite obtenemos la relación general

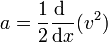
a = \frac{1}{2}\frac{\mathrm{d}\ }{\mathrm{d}x}(v^2)

esto es, en un movimiento uniformemente acelerado se obtiene una recta en la gráfica de v2 frente a x, no en la de v(x).

Podemos aplicar esta fórmula a los diferentes casos indicados en el enunciado:

Ferrari
En el primer tramo tenemos
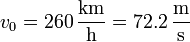
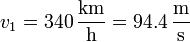
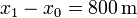
v_0 = 260\,\frac{\mathrm{km}}{\mathrm{h}} = 72.2\,\frac{\mathrm{m}}{\mathrm{s}}        v_1 = 340\,\frac{\mathrm{km}}{\mathrm{h}} = 94.4\,\frac{\mathrm{m}}{\mathrm{s}}        x_1-x_0 = 800\,\mathrm{m}
lo que nos da la aceleración
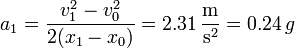
a_1 = \frac{v_1^2-v_0^2}{2(x_1-x_0)}=2.31\,\frac{\mathrm{m}}{\mathrm{s}^2} = 0.24\,g
En el segundo tramo, en que el movimiento es uniforme, la aceleración es nula.
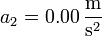
a_2 = 0.00\,\frac{\mathrm{m}}{\mathrm{s}^2}
En el tercer tramo operamos del mismo modo
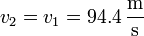
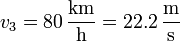
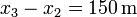
v_2 = v_1 = 94.4\,\frac{\mathrm{m}}{\mathrm{s}}        v_3 = 80\,\frac{\mathrm{km}}{\mathrm{h}} = 22.2\,\frac{\mathrm{m}}{\mathrm{s}}        x_3-x_2 = 150\,\mathrm{m}
y nos queda la aceleración
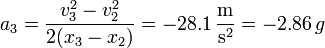
a_3 = \frac{v_3^2-v_2^2}{2(x_3-x_2)}= -28.1\,\frac{\mathrm{m}}{\mathrm{s}^2} = -2.86\,g
Vemos que la aceleración es mucho más intensa en la frenada que en el tramo acelerado.


Red Bull
Operando igualmente, en el primer tramo tenemos
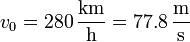
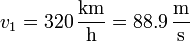
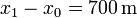
v_0 = 280\,\frac{\mathrm{km}}{\mathrm{h}} = 77.8\,\frac{\mathrm{m}}{\mathrm{s}}        v_1 = 320\,\frac{\mathrm{km}}{\mathrm{h}} = 88.9\,\frac{\mathrm{m}}{\mathrm{s}}        x_1-x_0 = 700\,\mathrm{m}
y queda la aceleración
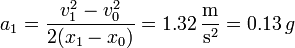
a_1 = \frac{v_1^2-v_0^2}{2(x_1-x_0)}=1.32\,\frac{\mathrm{m}}{\mathrm{s}^2} = 0.13\,g
En el segundo tramo la aceleración es nula.
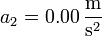
a_2 = 0.00\,\frac{\mathrm{m}}{\mathrm{s}^2}
y en el tercer tramo vale
v_2 = v_1 = 89.9\,\frac{\mathrm{m}}{\mathrm{s}}        v_3 = 90\,\frac{\mathrm{km}}{\mathrm{h}} = 25.0\,\frac{\mathrm{m}}{\mathrm{s}}        x_3-x_2 = 120\,\mathrm{m}
a_3 = \frac{v_3^2-v_2^2}{2(x_3-x_2)}= -30.3\,\frac{\mathrm{m}}{\mathrm{s}^2} = -3.10\,g

3 Velocidad media

Obtenido de "http://tesla.us.es/wiki/index.php/Aceleraci%C3%B3n_en_un_tramo_rectil%C3%ADneo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace