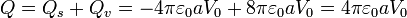Potencial eléctrico fuera de un conductor

De Laplace

(Diferencias entre revisiones)

Revisión de 23:03 2 jul 2011

Contenido

1 Enunciado
2 Radio de la esfera
3 Campo eléctrico
4 Densidades de carga
- 4.1 Volumétrica
- 4.2 Superficial
5 Carga total
- 5.1 Por el desarrollo multipolar
- 5.2 Por integración de la carga
6 Energía electrostática
- 6.1 A partir del potencial
- 6.2 A partir del campo

1 Enunciado

En el exterior de una esfera conductora puesta a tierra se encuentra una cierta densidad de carga eléctrica de forma que el potencial eléctrico en el exterior de la esfera tiene la expresión

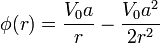
$\phi(r) = \frac{V_0a}{r}-\frac{V_0a^2}{2r^2}$

y es nulo en su interior.

Determine el radio de la esfera conductora.
Halle el campo eléctrico en todos los puntos del espacio.
Calcule las densidades de carga que son fuentes de este campo.
Halle la carga total de la distribución.
Calcule la energía electrostática almacenada en el sistema.

2 Radio de la esfera

El radio de la esfera lo calculamos sabiendo que éta se encuentra conectada a tierra y por tantu su tensión vale 0. Buscamos entonces en qué punto se anula el potencial

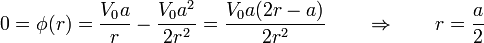
$0 = \phi(r) = \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} = \frac{V_0a(2r-a)}{2r^2}\qquad\Rightarrow\qquad r = \frac{a}{2}$

Por tanto, la esfera tiene radio $a / 2$ y la distribución del potencial es

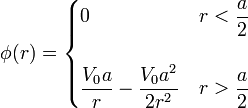
$\phi(r) = \begin{cases} 0 & r < \displaystyle\frac{a}{2} \\ & \\ \displaystyle \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} & r > \displaystyle \frac{a}{2}\end{cases}$

3 Campo eléctrico

Obtenemos el campo eléctrico como el gradiente del potencial, cambiado de signo.

En el interior de la esfera es nulo, mientras que en el exterior

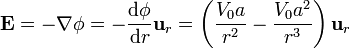
$\mathbf{E}=-\nabla\phi = -\frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_r = \left(\frac{V_0a}{r^2}-\frac{V_0a^2}{r^3}\right)\mathbf{u}_r$

Reuniendo los dos resultados

4 Densidades de carga

4.1 Volumétrica

La densidad de carga la poremos obtener a partir del campo eléctrico empleando la ley de Gauss

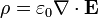
$\rho = \varepsilon_0\nabla\cdot\mathbf{E}$

Empleando la expresión en coordenadas esféricas

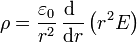
$\rho = \frac{\varepsilon_0}{r^2}\,\frac{\mathrm{d}\ }{\mathrm{d}r}\left(r^2E\right)$

En el interior de la esfera conductora esta densidad es naturalmente nula. En el exterior

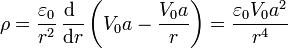
$\rho = \frac{\varepsilon_0}{r^2}\,\frac{\mathrm{d}\ }{\mathrm{d}r}\left(V_0a-\frac{V_0a}{r}\right) = \frac{\varepsilon_0 V_0a^2}{r^4}$

Alternativamente, podemos emplear la ecuación de Poisson

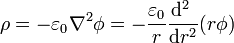
$\rho = -\varepsilon_0\nabla^2\phi = -\frac{\varepsilon_0}{r}\frac{\mathrm{d}^2\ }{\mathrm{d}r^2}(r\phi)$

Sustituyendo la expresión del potencial

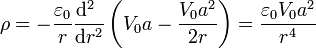
$\rho = -\frac{\varepsilon_0}{r}\frac{\mathrm{d}^2\ }{\mathrm{d}r^2}\left(V_0a-\frac{V_0a^2}{2r}\right) = \frac{\varepsilon_0 V_0a^2}{r^4}$

Combinando el resultado para el interior y el exterior

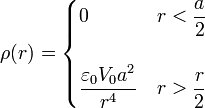
$\rho(r) = \begin{cases} 0 & r < \displaystyle\frac{a}{2} \\ & \\ \displaystyle \frac{\varepsilon_0 V_0a^2}{r^4} & r > \displaystyle \frac{r}{2}\end{cases}$

4.2 Superficial

Además de la densidad volumétrica tenemos una densidad superficial sobre la esfera conductora, que puede calcularse a partir de la discontinuidad en el campo eléctrico

$\sigma_s = \varepsilon_0\mathbf{n}\cdot[\mathbf{E}] = \varepsilon_0 \mathbf{u}_r\cdot\left(\mathbf{E}_\mathrm{ext}(a/2)-\mathbf{E}_\mathrm{int}(a/2)\right)$

Sustituyendo la expresión del campo eléctrico

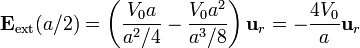
$\mathbf{E}_\mathrm{ext}(a/2) = \left(\frac{V_0a}{a^2/4}-\frac{V_0a^2}{a^3/8}\right)\mathbf{u}_r = -\frac{4V_0}{a}\mathbf{u}_r$

lo que nos da la densidad superficial de carga

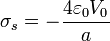
$\sigma_s = -\frac{4\varepsilon_0V_0}{a}$

5 Carga total

5.1 Por el desarrollo multipolar

La forma más sencilla de hallar la carga total es a partir del desarrollo multipolar. El potencial eléctrico exterior lo podemos escribir en la forma

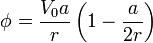
$\phi = \frac{V_0a}{r}\left(1-\frac{a}{2r}\right)$

cuando $r \gg a$ el segundo término del paréntesis es despreciable frente al primero, por lo que podemos aproximar el potencial por

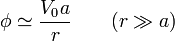
$\phi\simeq \frac{V_0a}{r}\qquad (r\gg a)$

Pero la dependencia como $1 / r$ identifica a este potencial como el de una carga puntual

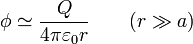
$\phi \simeq \frac{Q}{4\pi\varepsilon_0 r}\qquad (r\gg a)$

Identificando coeficientes

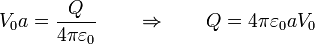
$V_0 a = \frac{Q}{4\pi\varepsilon_0}\qquad\Rightarrow\qquad Q = 4\pi\varepsilon_0a V_0$

Esta es la carga total de la distribución, ya que esta cantidad coincide con el momento monopolar de la distribución.

5.2 Por integración de la carga

De una manera más mecánica podemos hallar la carga integrando las densidades de carga que hemos obtenido previamente. Tenemos una carga almacenada en el volumen y otra en la superficie de la esfera conductora

La carga contenida en la superficie vale

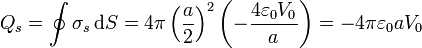
$Q_s = \oint \sigma_s\,\mathrm{d}S = 4\pi\left(\frac{a}{2}\right)^2 \left(-\frac{4\varepsilon_0V_0}{a}\right) = -4\pi \varepsilon_0aV_0$

y la del volumen

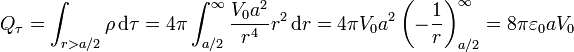
$Q_\tau = \int_{r>a/2}\rho\,\mathrm{d}\tau = 4\pi\int_{a/2}^\infty \frac{V_0a^2}{r^4}r^2\,\mathrm{d}r = 4\pi V_0a^2\left(-\frac{1}{r}\right)_{a/2}^\infty = 8\pi\varepsilon_0aV_0$

Sumando las dos cargas

$Q = Q_s+Q_v = -4\pi \varepsilon_0aV_0 + 8\pi \varepsilon_0a V_0 = 4\pi \varepsilon_0aV_0$

6 Energía electrostática

6.1 A partir del potencial

6.2 A partir del campo

@@ Línea 99: / Línea 99: @@
 y la del volumen
-<center><math>Q_\tau = \int_{r>a/2}\rho\,\mathrm{d}\tau = 4\pi\int_{a/2}^\infty \frac{V_0a^2}{r^4}r^2\,\mathrm{d}r = 4\pi V_0a^2\left(-\frac{1}{r}\right|_{a/2}^\infty = 8\pi\varepsilon_0aV_0</math></center>
+<center><math>Q_\tau = \int_{r>a/2}\rho\,\mathrm{d}\tau = 4\pi\int_{a/2}^\infty \frac{V_0a^2}{r^4}r^2\,\mathrm{d}r = 4\pi V_0a^2\left(-\frac{1}{r}\right)_{a/2}^\infty = 8\pi\varepsilon_0aV_0</math></center>
 Sumando las dos cargas

Potencial eléctrico fuera de un conductor

De Laplace

Revisión de 23:03 2 jul 2011

Contenido

1 Enunciado

2 Radio de la esfera

3 Campo eléctrico

4 Densidades de carga

4.1 Volumétrica

4.2 Superficial

5 Carga total

5.1 Por el desarrollo multipolar

5.2 Por integración de la carga

6 Energía electrostática

6.1 A partir del potencial

6.2 A partir del campo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES