Potencial eléctrico fuera de un conductor
De Laplace
(Diferencias entre revisiones)
(→=A partir del potencial) |
|||
| Línea 13: | Línea 13: | ||
==Radio de la esfera== | ==Radio de la esfera== | ||
| + | El radio de la esfera lo calculamos sabiendo que éta se encuentra conectada a tierra y por tantu su tensión vale 0. Buscamos entonces en qué punto se anula el potencial | ||
| + | |||
| + | <center><math>0 = \phi(r) = \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} = \frac{V_0a(2r-a)}{2r^2}\qquad\Rightarrow\qquad r = \frac{a}{2}</math></center> | ||
| + | |||
| + | Por tanto, la esfera tiene radio <math>a/2</math> y la distribución del potencial es | ||
| + | |||
| + | <center><math>\phi(r) = \begin{cases} 0 & r < \displaystyle\frac{a}{2} \\ & \\ \displaystyle \frac{V_0a}{r}-\frac{V_0a^2}{2r^2} & r > \displaystyle \frac{r}{2}\end{cases}</math></center> | ||
| + | |||
==Campo eléctrico== | ==Campo eléctrico== | ||
==Densidades de carga== | ==Densidades de carga== | ||
Revisión de 18:38 2 jul 2011
Contenido |
1 Enunciado
En el exterior de una esfera conductora puesta a tierra se encuentra una cierta densidad de carga eléctrica de forma que el potencial eléctrico en el exterior de la esfera tiene la expresión
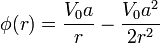
y es nulo en su interior.
- Determine el radio de la esfera conductora.
- Halle el campo eléctrico en todos los puntos del espacio.
- Calcule las densidades de carga que son fuentes de este campo.
- Halle la carga total de la distribución.
- Calcule la energía electrostática almacenada en el sistema.
2 Radio de la esfera
El radio de la esfera lo calculamos sabiendo que éta se encuentra conectada a tierra y por tantu su tensión vale 0. Buscamos entonces en qué punto se anula el potencial
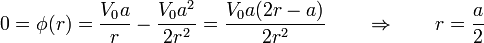
Por tanto, la esfera tiene radio a / 2 y la distribución del potencial es






