Energía electromagnética en una onda viajera
De Laplace
(Diferencias entre revisiones)
(→Campo magnético) |
|||
| Línea 22: | Línea 22: | ||
De acuerdo con la ley de Faraday, esto debe ser igual a la derivada temporal del campo magnético, cambiada de signo. | De acuerdo con la ley de Faraday, esto debe ser igual a la derivada temporal del campo magnético, cambiada de signo. | ||
| - | <center><math>-\frac{\partial\mathbf{B}}{\partial t} = k E_0\mathrm{sen}(\omega t - k z)\mathbf{u}_y\qquad\Rightarrow\qquad \mathbf{B}= | + | <center><math>-\frac{\partial\mathbf{B}}{\partial t} = k E_0\mathrm{sen}(\omega t - k z)\mathbf{u}_y\qquad\Rightarrow\qquad \mathbf{B}=\frac{k}{\omega}\cos(\omega t - k x)\mathbf{u}_y</math></center> |
| + | |||
| + | En principio la amplitud de las oscilaciones del campo magnético dependen tanto de la frecuencia <math>\omega</math> como del número de onda <math>k</math>. Sin embargo, no es así. Sustituyendo en la ley de Ampère-Maxwell obtenemos, por un lado | ||
| + | |||
| + | <center><math>\nabla\times\mathbf{B}=-\frac{k^2}{\omega}E_0\mathrm{sen}(\omega t - kx)\mathbf{u}_x</math></center> | ||
| + | |||
| + | y por otro | ||
| + | |||
| + | <center><math>\mu_0 \varepsilon_0\frac{\partial\mathbf{E}}{\partial t} = -\mu_0\varepsilon_0 \omega E_0\mathrm{sen}(\omega t - k z)\mathbf{u}_x</math></center> | ||
| + | |||
| + | Para que estas dos cantidades sean iguales en todo instante, debe ser | ||
| + | |||
| + | <center><math>\frac{k^2}{\omega} = \mu_0\varepsilon_0\omega \qquad\Rightarrow\qquad \omega = \frac{k}{\sqrt{\mu_0\\vareposilon_0}} = ck</math></center> | ||
| + | |||
| + | Esta es la llamada ''relación de dispersión'' para el vacío. De aquí obtenemos | ||
| + | |||
| + | <center><math>\mathbf{B} = \frac{E_0}{c}\cos(\omega t - k x)\mathbf{u}_y</math></center> | ||
| + | |||
| + | El campo magnético, por tanto, oscila completamente en fase con el campo eléctrico. | ||
| + | |||
==Densidades de energía== | ==Densidades de energía== | ||
==Promedio de la densidad de energía== | ==Promedio de la densidad de energía== | ||
Revisión de 21:15 1 jun 2011
Contenido |
1 Enunciado
Una onda plana monocromática en una región libre de fuentes posee el campo eléctrico
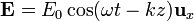
- Determine el valor del campo magnético en todos los puntos del espacio.
- Calcule las densidades de energía eléctrica y magnética en todos los puntos del espacio.
- Halle el promedio temporal de las densidades de energía, definido como
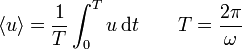
- Calcule el vector de Poynting en cada instante
- Halle el promedio temporal del vector de Poynting
2 Campo magnético
Si hallamos las fuentes vectoriales del campo eléctrico obtenemos
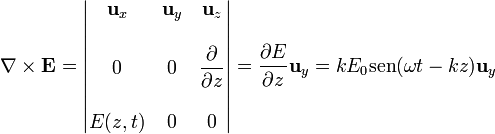
De acuerdo con la ley de Faraday, esto debe ser igual a la derivada temporal del campo magnético, cambiada de signo.
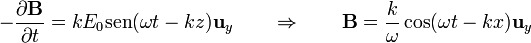
En principio la amplitud de las oscilaciones del campo magnético dependen tanto de la frecuencia ω como del número de onda k. Sin embargo, no es así. Sustituyendo en la ley de Ampère-Maxwell obtenemos, por un lado
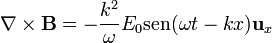
y por otro
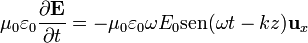
Para que estas dos cantidades sean iguales en todo instante, debe ser
Esta es la llamada relación de dispersión para el vacío. De aquí obtenemos
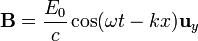
El campo magnético, por tanto, oscila completamente en fase con el campo eléctrico.





