Condensador relleno de un medio estratificado

De Laplace

(Diferencias entre revisiones)

Revisión de 21:32 21 may 2011

Contenido

1 Enunciado
2 Cálculo de los campos
3 Densidades de carga
4 Energía almacenada

1 Enunciado

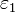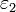Un medio estratificado es aquel cuyas propiedades dependen de la altura $z$ . Un material de este tipo se coloca entre dos placas conductoras planas y paralelas, separadas una distancia $a$ . La permitividad del material varía de $\varepsilon_1$ a $\varepsilon_2$ en la forma

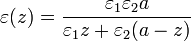
$\varepsilon(z)= \frac{\varepsilon_1\varepsilon_2a}{\varepsilon_1z+\varepsilon_2(a-z)}$

Si se aplica una diferencia de potencial $V 0$ entre las placas,

¿Cuánto valen los campos $\mathbf{D}$ , $\mathbf{E}$ y $\mathbf{P}$ en todos los puntos del material?
¿Cuál es la densidad de carga de polarización (tanto superficial como de volumen)?
Halle la energía almacenada en el sistema

Desprecie los efectos de borde.

2 Cálculo de los campos

Por tratarse de una situación electrostática y no haber carga libre en el dieléctrico, por ser este ideal, se cumple

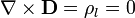
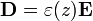
$\nabla\times\mathbf{D}=\rho_l=0$ $\nabla\times\mathbf{E}=\mathbf{0}$ $\mathbf{D}=\varepsilon(z) \mathbf{E}$

Si suponemos despreciables los efectos de borde y admitimos que los campos van en línea recta de una placa a la otra, escribimos el campo eléctrico y el vector desplazamiento como

$\mathbf{E}=E\mathbf{u}_z\qquad\qquad\mathbf{D}=D\mathbf{u}_z$

lo cual sustituyendo en las ecuaciones de la electrostática nos da, para la ley de Gauss

$0 = \nabla\cdot\mathbf{D} = 0 + 0 + \frac{\partial D}{\partial z}$

y para la irrotacionalidad del campo eléctrico

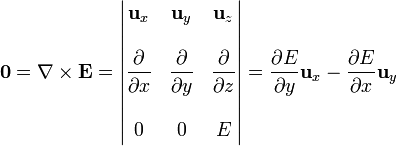
$\mathbf{0}=\nabla\times\mathbf{E}=\left|\begin{matrix} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\ & & \\ 0 & 0 & E\end{matrix}\right| = \frac{\partial E}{\partial y}\mathbf{u}_x - \frac{\partial E}{\partial x} \mathbf{u}_y$

puesto que un vector se anula cuando se anulan sus componentes, este sistema equivale a las ecuaciones

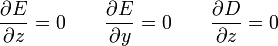
$\frac{\partial E}{\partial z} = 0 \qquad \frac{\partial E}{\partial y} = 0 \qquad \frac{\partial D}{\partial z} = 0$

Tenemos que el campo eléctrico no depende de las coordenadas transversales, mientra que el desplazamiento no depende de la coordenada normal a las placas. Sin embargo, ¿depende el campo eléctrico de z? ¿Depende D de x e y? Para eso precisamos la relación constitutiva. Si derivamos el campo eléctrico respecto a z obtenemos

$\frac{\partial E}{\partial z} = \frac{\partial }{\partial z}\left(\frac{D}{\varepsilon(z)}\right) = \frac{1}{\varepsilon(z)}\overbrace{\frac{\partial D}{\partial z}}^{=0}-\frac{D}{\varepsilon^2}\frac{\mathrm{d} \varepsilon}{\mathrm{d} z}\neq 0$

3 Densidades de carga

4 Energía almacenada

@@ Línea 37: / Línea 37: @@
 <center><math>\frac{\partial E}{\partial z} = 0 \qquad \frac{\partial E}{\partial y} = 0 \qquad \frac{\partial D}{\partial z} = 0</math></center>
+Tenemos que el campo eléctrico no depende de las coordenadas transversales, mientra que el desplazamiento no depende de la coordenada normal a las placas. Sin embargo, ¿depende el campo eléctrico de z? ¿Depende D de x e y? Para eso precisamos la relación constitutiva. Si derivamos el campo eléctrico respecto a z obtenemos
+<center><math>\frac{\partial E}{\partial z} = \frac{\partial }{\partial z}\left(\frac{D}{\varepsilon(z)}\right) = \frac{1}{\varepsilon(z)}\overbrace{\frac{\partial D}{\partial z}}^{=0}-\frac{D}{\varepsilon^2}\frac{\mathrm{d} \varepsilon}{\mathrm{d} z}\neq 0</math></center>
 ==Densidades de carga==
 ==Energía almacenada==
 [[Categoría:Problemas de materiales dieléctricos]]

Condensador relleno de un medio estratificado

De Laplace

Revisión de 21:32 21 may 2011

Contenido

1 Enunciado

2 Cálculo de los campos

3 Densidades de carga

4 Energía almacenada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES