Entrar Página Discusión Historial Go to the site toolbox

Condensador relleno de un medio estratificado

De Laplace

(Diferencias entre revisiones)
(→Cálculo de los campos)
(→Cálculo de los campos)
Línea 31: Línea 31:
y para la irrotacionalidad del campo eléctrico
y para la irrotacionalidad del campo eléctrico
-
<center><math>\mathbf{0}=\nabla\times\mathbf{E}=\left|\begin{array} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\ & & \\ 0 & 0 & E\end{array}\right| = \frac{\partial E}{\partial y}\mathbf{u}_x - \frac{\partial E}{\partial x} \mathbf{u}_y</math></center>
+
<center><math>\mathbf{0}=\nabla\times\mathbf{E}=\left|\begin{matrix} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\ & & \\ 0 & 0 & E\end{matrix}\right| = \frac{\partial E}{\partial y}\mathbf{u}_x - \frac{\partial E}{\partial x} \mathbf{u}_y</math></center>
puesto que un vector se anula cuando se anulan sus componentes, este sistema equivale a las ecuaciones
puesto que un vector se anula cuando se anulan sus componentes, este sistema equivale a las ecuaciones

Revisión de 17:04 21 may 2011

Contenido

1 Enunciado

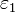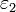Un medio estratificado es aquel cuyas propiedades dependen de la altura z. Un material de este tipo se coloca entre dos placas conductoras planas y paralelas, separadas una distancia a. La permitividad del material varía de \varepsilon_1 a \varepsilon_2 en la forma

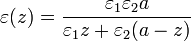
\varepsilon(z)= \frac{\varepsilon_1\varepsilon_2a}{\varepsilon_1z+\varepsilon_2(a-z)}

Si se aplica una diferencia de potencial V0 entre las placas,

  1. ¿Cuánto valen los campos \mathbf{D}, \mathbf{E} y \mathbf{P} en todos los puntos del material?
  2. ¿Cuál es la densidad de carga de polarización (tanto superficial como de volumen)?
  3. Halle la energía almacenada en el sistema

Desprecie los efectos de borde.

2 Cálculo de los campos

Por tratarse de una situación electrostática y no haber carga libre en el dieléctrico, por ser este ideal, se cumple

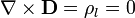
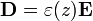
\nabla\times\mathbf{D}=\rho_l=0        \nabla\times\mathbf{E}=\mathbf{0}        \mathbf{D}=\varepsilon(z) \mathbf{E}

Si suponemos despreciables los efectos de borde y admitimos que los campos van en línea recta de una placa a la otra, escribimos el campo eléctrico y el vector desplazamiento como

\mathbf{E}=E\mathbf{u}_z\qquad\qquad\mathbf{D}=D\mathbf{u}_z

lo cual sustituyendo en las ecuaciones de la electrostática nos da, para la ley de Gauss

0 = \nabla\cdot\mathbf{D} = 0 + 0 + \frac{\partial D}{\partial z}

y para la irrotacionalidad del campo eléctrico

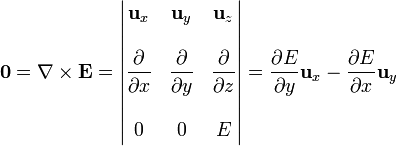
\mathbf{0}=\nabla\times\mathbf{E}=\left|\begin{matrix} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\ & & \\ 0 & 0 & E\end{matrix}\right| = \frac{\partial E}{\partial y}\mathbf{u}_x - \frac{\partial E}{\partial x} \mathbf{u}_y

puesto que un vector se anula cuando se anulan sus componentes, este sistema equivale a las ecuaciones

\frac{\partial E}{\partial z} = 0 \qquad \frac{\partial E}{\partial y} = 0 \qquad \frac{\partial D}{\partial z} = 0

3 Densidades de carga

4 Energía almacenada

Obtenido de "http://tesla.us.es/wiki/index.php/Condensador_relleno_de_un_medio_estratificado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace