Campo eléctrico entre dos cargas puntuales GIA

De Laplace

Revisión de 10:42 1 mar 2011

1 Enunciado

Se tienen dos cargas puntuales q₁ y q₂ separadas por una distancia d. Determina el punto sobre la línea que las une en el que el campo eléctrico se anula para cada uno de estos casos

1. .
2. .
3. .
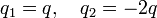4. q₁ y q₂ arbitrarios.

2 Solución

Vamos a hacer el caso general con valores arbitrarios de las cargas. Consideramos una carga q situada en una posición arbitraria del eje OX dada por la coordenada x₁. El campo que produce en un punto Pcualquiera de ese eje es

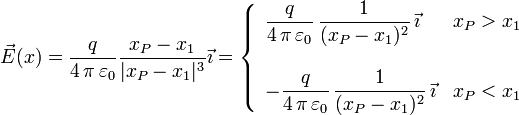
Si q > 0 el campo apunta hacia la derecha a la derecha de la carga (x_P > x₁) y hacia la izquierda a la izquierda de la carga (x_P < x₁).

Si tenemos dos cargas, q₁ y q₂ situadas en los puntos del eje OX de coordenadas respectivas x₁ y x₂ respectivamente, el campo total en un punto P arbitrario del eje es la suma de los campos de las dos cargas. Para simplificar, vamos a situar el origen en la posición de la carga q₁, (x₁ = 0) y que la otra carga está a su derecha (x₂ > 0). El campo de cada carga es

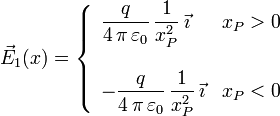
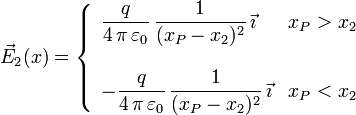
Hay que distinguir tres zonas en el eje eje, a la izquierda de q₁, entre las dos cargas y a la derecha de q₂. Estas tres zonas vienen dadas por (x_P < 0), 0 < x_P < x₂ y x_P > x₂, respectivamente.