6.8. Barra horizontal apoyada en disco
De Laplace
| Línea 46: | Línea 46: | ||
==Aceleración== | ==Aceleración== | ||
| - | La aceleración de A la podemos hallar mediante la | + | La aceleración de A la podemos hallar mediante la composición de movimientos |
| - | \vec{a}^A_{20}= | + | <center><math>\vec{a}^A_{21}=\vec{a}^A_{20}+\vec{a}^A_{01}+2\omega_{01}\vec{k}\times\vec{v}^A_{21}</math></center> |
| + | |||
| + | de donde, despejando, | ||
| + | |||
| + | <center><math>\vec{a}^A_{20}=\vec{a}^A_{21}-\vec{a}^A_{01}-2\omega_{01}\vec{k}\times\vec{v}^A_{21}</math></center> | ||
| + | |||
| + | El movimiento {21} del punto A es una traslación a velocidad constante, por lo que su aceleración es nula | ||
| + | |||
| + | <center><math>\vec{a}^A_{21}=\frac{\mathrm{d}v_0}{\mathrm{d}t}\vec{\imath}_1 = \vec{0}</math></center> | ||
| + | |||
| + | La aceleración en el movimiento {01} no puede calcularse derivando, porque el punto A es una partícula material diferente en cada instante. Aplicamos la reducción en O del campo de aceleraciones, por ser O un punto material perfectamente definido | ||
| + | |||
| + | <center><math>\vec{a}^A_{01}=\vec{a}^A_{01}+\alpha_{01}\vec{k}\times\overrightarrow{OA}-\omega_{01}^2\overrightarrow{OA}</math></center> | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 18:20 9 ene 2011
Contenido |
1 Enunciado
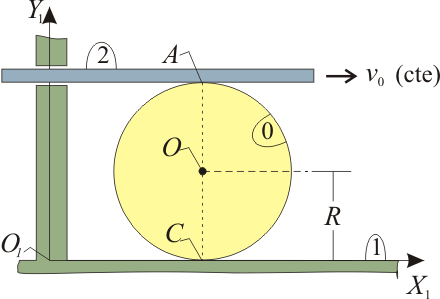
El sistema de la figura consta de un disco (sólido “0”), de centro O y radio R, que rueda sin deslizar sobre el eje horizontal O1X1 de la escuadra fija O1X1Y1 (sólido “1”); y de una barra de longitud indefinida (sólido “2”), que se desplaza horizontalmente con velocidad constante v0, manteniéndose siempre en contacto tangente con el perímetro del disco (punto A) y sin deslizar sobre éste. Se pide:
- Reducciones cinemáticas de los movimientos {21}, {01} y {20} en el centro del disco (punto O), es decir:
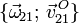 ,
, 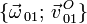 y
y 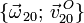 .
.
- Aceleración relativa barra-disco del punto de contacto A, es decir:
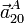 .
.
2 Reducciones cinemáticas
2.1 Movimiento {21}
La barra “2” efectúa un movimiento de traslación respecto al sólido “1”, por lo que la velocidad angular de este movimiento es nula y la velocidad de traslación es la misma para todos los puntos, en particular el centro del disco, O.
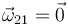
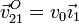
2.2 Movimiento {01}
Al ser el contacto entre el disco y el eje horizontal una rodadura sin deslizamiento, el movimiento relativo es una rotación en torno a este punto. Por ello
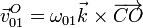
La velocidad angular la obtenemos de que podemos hallar la velocidad del punto B, de contacto del disco y la barra, en el movimiento {01}, por ser este contacto también una rodadura sin deslizamiento
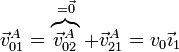
La velocidad de este punto cumple igualmente
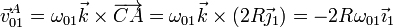
Igualando las dos expresiones obtenemos la velocidad angular
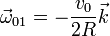
y la velocidad del punto O
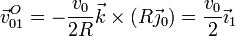
2.3 Movimiento {20}
Una vez que tenemos dos de las reducciones cinemáticas, podemos hallar la tercera mediante la composición de movimientos. Para la velocidad angular
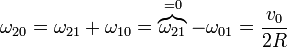
y para la lineal
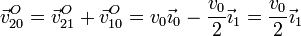
3 Aceleración
La aceleración de A la podemos hallar mediante la composición de movimientos
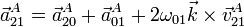
de donde, despejando,
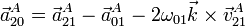
El movimiento {21} del punto A es una traslación a velocidad constante, por lo que su aceleración es nula
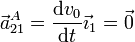
La aceleración en el movimiento {01} no puede calcularse derivando, porque el punto A es una partícula material diferente en cada instante. Aplicamos la reducción en O del campo de aceleraciones, por ser O un punto material perfectamente definido






