6.2. Movimiento de barra en un pasador
De Laplace
(→Determinación gráfica del CIR) |
|||
| Línea 14: | Línea 14: | ||
Alternativamente, con ayuda del teorema de los tres centros, puede sustituirse alguna (o las dos) de las rectas perpendiculares anteriores por una recta que pasa por dos CCIIR conocidos. | Alternativamente, con ayuda del teorema de los tres centros, puede sustituirse alguna (o las dos) de las rectas perpendiculares anteriores por una recta que pasa por dos CCIIR conocidos. | ||
| + | |||
| + | [[Archivo:varilla-pasador-02.png|right]] | ||
En este problema tenemos un punto del cual es inmediata la dirección de movimiento: el punto A se mueve según una recta horizontal, de forma que | En este problema tenemos un punto del cual es inmediata la dirección de movimiento: el punto A se mueve según una recta horizontal, de forma que | ||
| Línea 25: | Línea 27: | ||
<center><math>\vec{v}^C_{21}=v^C\vec{\jmath}_2</math></center> | <center><math>\vec{v}^C_{21}=v^C\vec{\jmath}_2</math></center> | ||
| - | Trazamos entonces la perpendicular a la barra por C, resultando una recta | + | Trazamos entonces la perpendicular a la barra por C, resultando una recta paralela al eje <center><math>OX_2</math></center> |
| + | |||
| + | La intersección de estas dos rectas nos da el centro instantáneo de rotación. Este punto está situado sobre la vertical de A en el sistema “1”. Podemos hallar la altura a la que se encuentra por simples razonamientos trigonométricos. | ||
| + | |||
| + | La altura <math>a</math> que da el enunciado es el cateto contiguo de un triángulo con ángulo <math>\theta</math> en el vértice. la hipotenusa de este triángulo vale | ||
| + | |||
| + | <center><math>L = \frac{a}{\cos\theta}</math></center> | ||
| + | |||
| + | A su vez este lado es un cateto contiguo de otro | ||
| + | |||
==Velocidades y aceleraciones== | ==Velocidades y aceleraciones== | ||
==Obtención analítica del CIR== | ==Obtención analítica del CIR== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 20:53 19 dic 2010
Contenido |
1 Enunciado
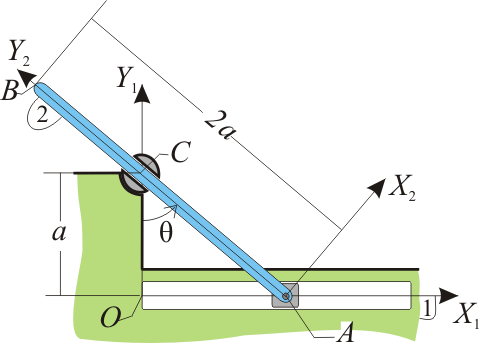
La barra AB (sólido “2”), de longitud 2a, puede deslizar en su extremo A por el eje OX1 de la escuadra fija OX1Y1 (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje OY1, a una distancia a del origen O. Sabiendo que la barra gira con velocidad angular constante Ω (ley horaria θ(t) = Ωt, donde θ es el ángulo definido en la figura), se pide:
- Determinar gráficamente la posición del centro instantáneo de rotación (CIR) del movimiento {21}.
- Calcular las velocidades,
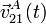y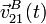 
, y las aceleraciones, 
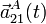y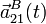 
, de los dos extremos de la barra en cualquier instante de tiempo.
- Determinar analíticamente la posición del C.I.R. del movimiento {21}.
2 Determinación gráfica del CIR
En la mayoría de los problemas de movimiento plano, existe más de una forma de determinar geométricamente la posición del centro instantáneo de rotación.
El procedimiento habitual suele ser buscar dos puntos para los cuales se conoce la dirección de la velocidad, trazar las perpendiculares a estas direcciones y localizar la intersección de estas rectas.
Alternativamente, con ayuda del teorema de los tres centros, puede sustituirse alguna (o las dos) de las rectas perpendiculares anteriores por una recta que pasa por dos CCIIR conocidos.
En este problema tenemos un punto del cual es inmediata la dirección de movimiento: el punto A se mueve según una recta horizontal, de forma que
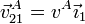
El CIR se encontrará entonces según la perpendicular por A a esta velocidad. Esta perpendicular es una recta paralela al eje OY1.
Como segundo punto consideramos el punto C en el que la barra se encuentra vinculada. El pasador establece un vínculo bilateral que impide que la barra se mueva perpendicularmente a sí misma (ya que en ese caso chocaría con el pasador). Por tanto la velocidad de C es a lo largo de la propia barra
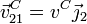
La intersección de estas dos rectas nos da el centro instantáneo de rotación. Este punto está situado sobre la vertical de A en el sistema “1”. Podemos hallar la altura a la que se encuentra por simples razonamientos trigonométricos.
La altura a que da el enunciado es el cateto contiguo de un triángulo con ángulo θ en el vértice. la hipotenusa de este triángulo vale
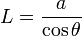
A su vez este lado es un cateto contiguo de otro
