Ejemplo paramétrico de movimiento plano
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== La escuadra <math>O_2X_2Y_2</math> (sólido “2”) se mueve respecto a la escuadra <math>O_1X_1Y_1</math> (sólido “1”) de forma que su orig…') |
|||
| Línea 11: | Línea 11: | ||
==Velocidad y aceleración== | ==Velocidad y aceleración== | ||
| + | ===Velocidad=== | ||
| + | La velocidad del punto <math>O_1</math>, como parte del sólido “2” respecto al “1”, <center><math>\vec{v}^{O_1}_{21}</math></center> puede calcularse de diferentes formas. | ||
| + | |||
| + | ====Empleando el sistema de referencia “1”=== | ||
| + | Debemos hallar la velocidad cuya posición no conocemos en todo instante. El punto cuya posición sí conocemos y podemos derivar es <math>O_2</math>. Por ello, debemos usar la expresión del campo de velocidades | ||
| + | |||
| + | <center><math>\vec{v}^{O_1}_{21}=\vec{v}^{O_2}_{21} + \omega_{21}\vec{k}\times\overrightarrow{O_2O_1}</math></center> | ||
| + | |||
| + | Veamos cada término por separado. | ||
| + | |||
| + | La velocidad de <center><math>O_2</math></center> en el movimiento {21} sí puede hallarse derivando respecto al tiempo, por aplicación de la regla de la cadena. | ||
| + | |||
| + | <center><math>\vec{v}^{O_2}_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{O_1O_2}\right|_1=A\dot{\theta}\theta\left(\cos(\theta)ºvec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\right)</math></center> | ||
==CIR en el sistema “1”== | ==CIR en el sistema “1”== | ||
==CIR en el sistema “2”== | ==CIR en el sistema “2”== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 17:38 16 dic 2010
Contenido |
1 Enunciado
La escuadra O2X2Y2 (sólido “2”) se mueve respecto a la escuadra O1X1Y1 (sólido “1”) de forma que su origen de coordenadas, O2, verifica la ecuación paramétrica
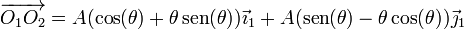
siendo θ = θ(t) el ángulo que el eje O2X2 forma con el O1X1.
- Calcule la velocidad y la aceleración instantáneas del punto O1 en el movimiento {21}:
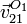 y
y 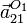 .
.
- Determine la posición del CIR I21 y exprésela empleando el sistema de referencia ligado al sólido “1”.
- Exprese la posición del mismo punto I21 en el sistema de referencia ligado al sólido “2”.
2 Velocidad y aceleración
2.1 Velocidad
La velocidad del punto O1, como parte del sólido “2” respecto al “1”,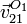
2.2 =Empleando el sistema de referencia “1”
Debemos hallar la velocidad cuya posición no conocemos en todo instante. El punto cuya posición sí conocemos y podemos derivar es O2. Por ello, debemos usar la expresión del campo de velocidades
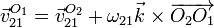
Veamos cada término por separado.
La velocidad de





