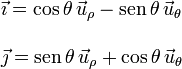Coordenadas polares
De Laplace
(→Relación con las coordenadas cartesianas) |
(→Relación con las coordenadas cartesianas) |
||
| Línea 49: | Línea 49: | ||
|style="border: 1px solid black;"| <math>\theta = \mathrm{arctan}(y/x) </math> | |style="border: 1px solid black;"| <math>\theta = \mathrm{arctan}(y/x) </math> | ||
|} | |} | ||
| + | </center> | ||
| + | |||
| + | == Base vectorial en polares == | ||
| + | |||
| + | Al igual que el sistema de coordenadas cartesianas, las coordenadas polares | ||
| + | llevan asociada una base vectorial. Esta base la componen los vectores unitarios | ||
| + | <math>\{\vec{u}_{\rho},\vec{u}_{\theta} \} </math> pintados en verde en la figura. | ||
| + | |||
| + | El vector <math>\vec{u}_{\rho} </math> apunta en la dirección y sentido | ||
| + | en que nos movemos si variamos la coordenada <math>\rho </math> manteniendo | ||
| + | <math> \theta</math> constante. Si <math>\rho </math> aumenta nos alejamos | ||
| + | radialmente del punto <math>O </math>, y si disminuye nos dirigimos hacia | ||
| + | <math>O </math>. | ||
| + | |||
| + | De igual modo, el vector <math>\vec{u}_{\theta} </math> apunta en la | ||
| + | dirección y sentido en que nos movemos si varía <math>\theta </math> | ||
| + | manteniendo <math>\rho </math> constante. Si <math>\theta </math> aumenta | ||
| + | nos desplazamos sobre la tangente a la circunferencia de radio <math>\rho </math> centrada en <math>O </math>, en sentido contrario a las agujas del | ||
| + | reloj. Si <math>\theta </math> disminuye el sentido del desplazamiento | ||
| + | es el de las agujas del reloj. | ||
| + | |||
| + | Usando los ángulos indicados en la figura podemos expresar los vectores de | ||
| + | la base polar en función de los vectores de la base cartesiana | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \vec{u}_{\rho} = \cos\theta\,\vec{\imath} + \mathrm{sen}\,\theta\,\vec{\jmath}\\ \\ | ||
| + | \vec{u}_{\theta} = -\mathrm{sen}\,\theta\,\vec{\imath} + \cos\theta\,\vec{\jmath} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | [[Imagen:Coordenadas_polares_vectores_polares_variables.png|right]] | ||
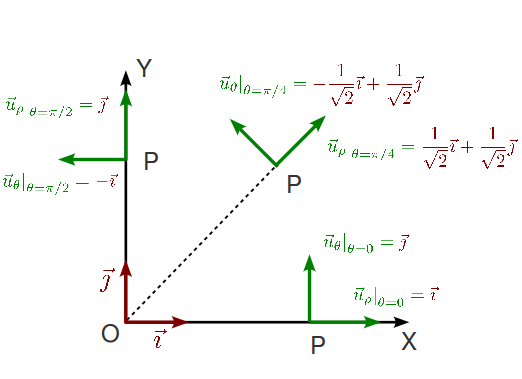
| + | Hay que destacar que, a diferencia de los vectores de la base cartesiana, | ||
| + | los vectores de la base polar '''no son constantes'''. Esto quiere decir | ||
| + | que varían en dirección y sentido al cambiar de punto en el plano. Algunos | ||
| + | ejemplos | ||
| + | <center> | ||
| + | {| style="text-align: center; width : 400px; height: 200px; border: 1px solid black; cellpading='5'" | ||
| + | |- | ||
| + | |style="border: 1px solid black; background: lavender"| <math>\theta </math> | ||
| + | |style="border: 1px solid black; background: lavender"| <math>\vec{u}_{\rho} </math> | ||
| + | |style="border: 1px solid black; background: lavender"| <math>\vec{u}_{\theta} </math> | ||
| + | |- | ||
| + | |style="border: 1px solid black;width : 400px;"| 0 | ||
| + | |style="border: 1px solid black;"| <math>\vec{\imath} </math> | ||
| + | |style="border: 1px solid black;"| <math>\vec{\jmath} </math> | ||
| + | |- | ||
| + | |style="border: 1px solid black;width : 400px;"| <math>\pi/4 </math> | ||
| + | |style="border: 1px solid black;"| <math>\dfrac{1}{\sqrt{2}}\vec{\imath} + \dfrac{1}{\sqrt{2}}\vec{\jmath} </math> | ||
| + | |style="border: 1px solid black;"| <math>-\dfrac{1}{\sqrt{2}}\vec{\imath} + \dfrac{1}{\sqrt{2}}\vec{\jmath} </math> | ||
| + | |- | ||
| + | |style="border: 1px solid black;width : 400px;"| <math>\pi/2 </math> | ||
| + | |style="border: 1px solid black;"| <math>\vec{\jmath} </math> | ||
| + | |style="border: 1px solid black;"| <math>-\vec{\imath} </math> | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | Podemos obtener la expresión de los vectores de la base cartesiana en función de la base polar proyectando en la primera figura o despejando en la expresión de los vectores polares en función de los cartesianos. Así | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \vec{\imath} = \cos\theta\,\vec{u}_{\rho} - \mathrm{sen}\,\theta\,\vec{u}_{\theta} \\ \\ | ||
| + | \vec{\jmath} = \mathrm{sen}\,\theta\,\vec{u}_{\rho} + \cos\theta\,\vec{u}_{\theta} | ||
| + | \end{array} | ||
| + | </math> | ||
</center> | </center> | ||
Revisión de 12:25 23 nov 2010
1 Definición
En el caso del movimiento bidimensional de un punto material resulta útil en muchas ocasiones trabajar con coordenadas polares. Usaremos la figura para definirlas.
Sea un punto P situado en el plano OXY con coordenadas cartesianas (x,y). Su vector de posición respecto al origen del sistema de referencia es
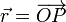
Las coordenadas polares (ρ,θ) se definen de la siguiente forma
- La coordenada ρ es la distancia del punto P al punto O. Puede variar entre los valores 0 y
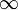 .
.
- La coordenada θ es el ángulo que forma el vector
 con el eje OX. Puede variar entre los valores 0 y 2π.
con el eje OX. Puede variar entre los valores 0 y 2π.
Estas dos coordenadas permiten describir de forma unívoca la posición de cualquier punto en el plano OXY.
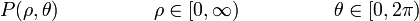
El intervalo para θ es abierto a la derecha para evitar llegar al valor de 2π. De lo contrario, los puntos del eje OX aparecerían dos veces, para θ = 0 y para θ = 2π.
2 Relación con las coordenadas cartesianas
Cada par de valores (x,y) corresponde unívocamente a un par de valores ρ,θ. La relación entre estos dos pares puede obtenerse a partir de la figura. Teniendo en cuenta el triángulo rectángulo formado por los catetos de longitud x e y y la hipotenusa de longitud ρ tenemos
| Polares → cartesianas | Cartesianas → polares |
|---|---|
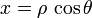
| 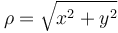
|
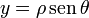
| θ = arctan(y / x) |
3 Base vectorial en polares
Al igual que el sistema de coordenadas cartesianas, las coordenadas polares
llevan asociada una base vectorial. Esta base la componen los vectores unitarios
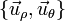 pintados en verde en la figura.
pintados en verde en la figura.
El vector 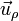 apunta en la dirección y sentido
en que nos movemos si variamos la coordenada ρ manteniendo
θ constante. Si ρ aumenta nos alejamos
radialmente del punto O, y si disminuye nos dirigimos hacia
O.
apunta en la dirección y sentido
en que nos movemos si variamos la coordenada ρ manteniendo
θ constante. Si ρ aumenta nos alejamos
radialmente del punto O, y si disminuye nos dirigimos hacia
O.
De igual modo, el vector 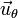 apunta en la
dirección y sentido en que nos movemos si varía θ
manteniendo ρ constante. Si θ aumenta
nos desplazamos sobre la tangente a la circunferencia de radio ρ centrada en O, en sentido contrario a las agujas del
reloj. Si θ disminuye el sentido del desplazamiento
es el de las agujas del reloj.
apunta en la
dirección y sentido en que nos movemos si varía θ
manteniendo ρ constante. Si θ aumenta
nos desplazamos sobre la tangente a la circunferencia de radio ρ centrada en O, en sentido contrario a las agujas del
reloj. Si θ disminuye el sentido del desplazamiento
es el de las agujas del reloj.
Usando los ángulos indicados en la figura podemos expresar los vectores de la base polar en función de los vectores de la base cartesiana
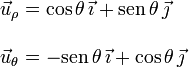
Hay que destacar que, a diferencia de los vectores de la base cartesiana, los vectores de la base polar no son constantes. Esto quiere decir que varían en dirección y sentido al cambiar de punto en el plano. Algunos ejemplos
| θ | 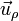
| 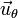
|
| 0 | 
| 
|
| π / 4 | 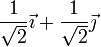
| 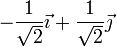
|
| π / 2 | 
| 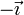
|
Podemos obtener la expresión de los vectores de la base cartesiana en función de la base polar proyectando en la primera figura o despejando en la expresión de los vectores polares en función de los cartesianos. Así