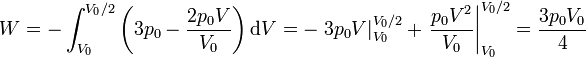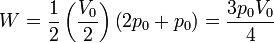Compresión lineal
De Laplace
| Línea 35: | Línea 35: | ||
==Trabajo, energía y calor== | ==Trabajo, energía y calor== | ||
| + | ===Trabajo=== | ||
| + | El trabajo realizado sobre el gas en un proceso reversible es igual a la integral | ||
| + | |||
| + | <center><math>W = - \int_{V_i}^{V_f}p\,\mathrm{d}V</math></center> | ||
| + | |||
| + | En nuestro caso | ||
| + | |||
| + | <center><math>W= -\int_{V_0}^{V_0/2} \left(3p_0-\frac{2p_0V}{V_0}\right)\mathrm{d}V = -\left.3p_0V\right|_{V_0}^{V_0/2}+\left.\frac{p_0V^2}{V_0}\right|_{V_0}^{V_0/2} = \frac{3p_0V_0}{4}</math></center> | ||
| + | |||
| + | Es muy fácil llegar a este resultado de forma gráfica, ya que el área bajo la curva es la de un trapecio de altura <center><math>V_0/2</math></center>, base menor <math>p_0</math> y base mayor <math>2p_0</math>. El área de este trapecio es | ||
| + | |||
| + | <center><math>W = \frac{1}{2}\left(\frac{V_0}{2}\right)\left(2p_0+p_0\right) = \frac{3p_0V_0}{4}</math></center> | ||
==Temperatura máxima== | ==Temperatura máxima== | ||
==División en dos tramos== | ==División en dos tramos== | ||
[[Categoría:Problemas del gas ideal]] | [[Categoría:Problemas del gas ideal]] | ||
Revisión de 16:55 16 nov 2010
Contenido |
1 Enunciado
Se tiene un volumen V0 de un gas ideal diatómico a una presión p0 y una temperatura T0 encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley
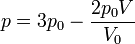
reduciéndose el volumen hasta V0 / 2.
- Trace la gráfica del proceso en un diagrama PV.
- Calcule la temperatura final del proceso.
- Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
- ¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima.
- Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.
2 Representación gráfica
Dado que la presión depende del volumen en la forma
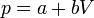
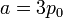

es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es (p0,V0) y el punto final corresponde a V = V0 / 2 y a la presión
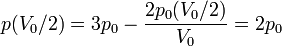
Por tanto el volumen final es la mitad del inicial, mientras que la presión es el doble.
3 Temperatura final
Obtenemos la temperatura final a partir de la ecuación de los gases ideales. Inicialmente tenemos
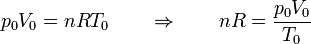
En el estado final
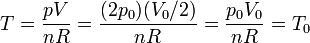
Por tanto, la temperatura final es igual a la inicial.
4 Trabajo, energía y calor
4.1 Trabajo
El trabajo realizado sobre el gas en un proceso reversible es igual a la integral
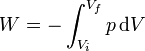
En nuestro caso