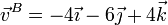4.4. Sólido en rotación instantánea
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto <math>A(1,0,-1)</math> y lleva la dirección del vector <math>\…') |
|||
| Línea 11: | Línea 11: | ||
==Valor de la constante== | ==Valor de la constante== | ||
| + | Por ser A un punto del eje instantáneo de rotacion, EIR | ||
| + | |||
| + | <center><math>\vec{v}^A = \vec{0}</math></center> | ||
| + | |||
| + | y la velocidad de cualquier otro punto, en particular B, verifica | ||
| + | |||
| + | <center><math>\vec{v}^B = \omega\times\overrightarrow{AB}</math></center> | ||
| + | |||
| + | Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante | ||
| + | |||
| + | <center><math>\vec{\omega}\parallel \vec{c}=2\vec{\imath}-2\vec{\jmath}-\vec{k}</math>{{tose}}<math>0 = \vec{v}^B\cdot\vec{c}=-8+12-c</math>{{tose}}<math>c=4\,</math></center> | ||
| + | |||
| + | y resulta la velocidad para el punto B | ||
| + | |||
| + | <center><math>\vec{v}^B = -4\vec{\imath}-6\vec{\jmath}+4\vec{k}</math></center> | ||
==Velocidad angular instantánea== | ==Velocidad angular instantánea== | ||
==Velocidad del punto C== | ==Velocidad del punto C== | ||
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]] | ||
Revisión de 14:38 13 nov 2010
Contenido |
1 Enunciado
Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector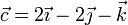 
, de tal forma que la velocidad del punto B(0,2,1) es
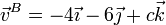
- Halle el valor de la constante c.
- Calcule la velocidad angular instantánea.
- Calcule la velocidad del punto C(1,1,0).
Todas las cantidades están expresadas en las unidades del SI.
2 Valor de la constante
Por ser A un punto del eje instantáneo de rotacion, EIR
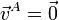
y la velocidad de cualquier otro punto, en particular B, verifica
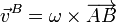
Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante
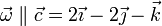
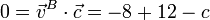
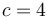
y resulta la velocidad para el punto B
