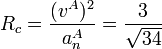4.7. Ejemplo de movimiento de precesión

De Laplace

(Diferencias entre revisiones)

Revisión de 18:37 9 nov 2010

Contenido

1 Enunciado
2 Campo de velocidades
3 Campo de aceleraciones
4 Componentes intrínsecas

1 Enunciado

El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular

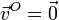
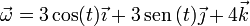
$\vec{v}^O = \vec{0}$ $\vec{\omega}=3\cos(t)\vec{\imath}+3\,\mathrm{sen}\,(t)\vec{\jmath}+4\vec{k}$

Determine el campo de velocidades del sólido.
Determine el campo de aceleraciones del sólido. ¿Es la aceleración de un punto igual a la derivada de la velocidad en ese punto respecto al tiempo?
Halle, para cada instante las componentes intrínsecas de la aceleración y el radio de curvatura en el punto

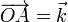
$\overrightarrow{OA}=\vec{k}$

2 Campo de velocidades

Por tratarse de una rotación pura

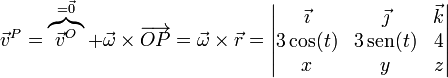
$\vec{v}^P = \overbrace{\vec{v}^O}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{OP}=\vec{\omega}\times\vec{r}= \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k}\\ 3\cos(t) & 3\,\mathrm{sen}(t) & 4 \\ x & y & z\end{matrix}\right|$

Separando en componentes cartesianas

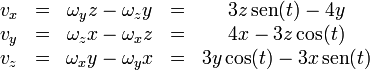
$\begin{matrix} v_x & = & \omega_y z - \omega_z y & = &3z\,\mathrm{sen}(t)-4y\\ v_y & = & \omega_z x - \omega_x z & = &4x - 3z\cos(t)\\ v_z & = & \omega_x y - \omega_y x & = &3y\cos(t)-3x\,\mathrm{sen}(t) \end{matrix}$

3 Campo de aceleraciones

El campo de aceleraciones tiene la expresión general

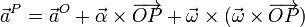
$\vec{a}^P = \vec{a}^O + \vec{\alpha}\times\overrightarrow{OP}+\vec{\omega}\times(\vec{\omega}\times\overrightarrow{OP})$

En este caso la aceleración de O es nula, por estar permanentemente en reposo, mientras que la aceleración angular vale

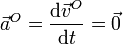
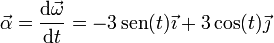
$\vec{a}^O = \frac{\mathrm{d}\vec{v}^O}{\mathrm{d}t}=\vec{0}$ $\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}=-3\,\mathrm{sen}(t)\vec{\imath}+3\cos(t)\vec{\jmath}$

Sustituyendo y separando en componentes cartesianas obtenemos

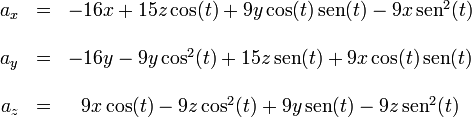
$\begin{matrix} a_x & = & -16x + 15z\cos(t)+9 y \cos(t)\,\mathrm{sen}(t)-9 x \,\mathrm{sen}^2(t)\\ && \\ a_y & = & -16 y-9 y \cos^2(t)+15 z \,\mathrm{sen}(t)+9 x \cos(t) \,\mathrm{sen}(t)\\ && \\ a_z & = & 9 x \cos(t)-9 z \cos^2(t)+9 y \,\mathrm{sen}(t)-9 z \,\mathrm{sen}^2(t) \end{matrix}$

Puede comprobarse de manera inmediata que

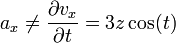
$a_x \neq \frac{\partial v_x}{\partial t}=3z\cos(t)$

y lo mismo ocurre para el resto de las componentes. ¿Por qué pasa esto si sabemos que la aceleración de una partícula es la derivada de su velocidad respecto al tiempo? La razón es que no estamos derivando bien respecto al tiempo. La expresión de la velocidad no sólo depende del tiempo explícitamente, sino que también lo hace de forma implícita a través de las coordenadas posicionales $x$ , $y$ y $z$ , las cuales varían al desplazarse la partícula. Por tanto, si se desea obtener la aceleración a partir de la velocidad, será necesario realizar la derivada total respecto al tiempo utilizando la regla de la cadena.

4 Componentes intrínsecas

Particularizando para $x = y = 0$ , $z = 1$ obtenemos

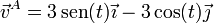
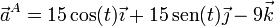
$\vec{v}^A = 3\,\mathrm{sen}(t)\vec{\imath}-3\cos(t)\vec{\jmath}$ $\vec{a}^A = 15\cos(t)\vec{\imath}+15\,\mathrm{sen}(t)\vec{\jmath}-9\vec{k}$

Una vez que tenemos los vectores velocidad aceleración podemos hallar las componentes intrínsecas de la aceleración.

Aceleración tangencial: Proyectando sobre la velocidad

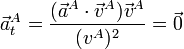
$\vec{a}^A_t = \frac{(\vec{a}^A\cdot\vec{v}^A)\vec{v}^A}{(v^A)^2} = \vec{0}$

Aceleración normal: Puesto que la aceleración tangencial es nula, toda la aceleración es normal

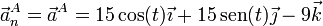
$\vec{a}^A_n = \vec{a}^A = 15\cos(t)\vec{\imath}+15\,\mathrm{sen}(t)\vec{\jmath}-9\vec{k}$

Radio de curvatura: Es inmediato conocida la aceleración normal y la celeridad

$R_c = \frac{(v^A)^2}{a^A_n} = \frac{3}{\sqrt{34}}$

@@ Línea 46: / Línea 46: @@
 <center><math>a_x \neq \frac{\partial v_x}{\partial t}=3z\cos(t)</math></center>
-y lo mismo para el resto de las componentes: la aceleración de un punto no es igual a la derivada de la velocidad instantánea de dicho punto respecto al tiempo. La razón es que al tener una velocidad no solo cambia la velocidad porque varía <math>t</math>. También <math>x</math>, <math>y</math> y <math>z</math> varían al desplazarse la partícula y por tanto deben ser incluidas en la derivación respecto al tiempo mediante la regla de la cadena.
+y lo mismo ocurre para el resto de las componentes. ¿Por qué pasa esto si sabemos que la aceleración de una partícula es la derivada de su velocidad respecto al tiempo? La razón es que no estamos derivando bien respecto al tiempo. La expresión de la velocidad no sólo depende del tiempo explícitamente, sino que también lo hace de forma implícita a través de las coordenadas posicionales <math>x</math>, <math>y</math> y <math>z</math>, las cuales varían al desplazarse la partícula. Por tanto, si se desea obtener la aceleración a partir de la velocidad, será necesario realizar la derivada total respecto al tiempo utilizando la regla de la cadena.
 ==Componentes intrínsecas==

4.7. Ejemplo de movimiento de precesión

De Laplace

Revisión de 18:37 9 nov 2010

Contenido

1 Enunciado

2 Campo de velocidades

3 Campo de aceleraciones

4 Componentes intrínsecas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES