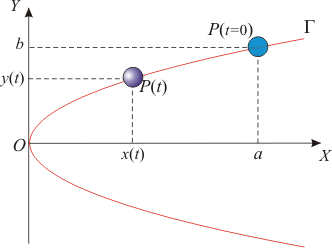
Partícula oscilando en parábola

De Laplace

(Diferencias entre revisiones)

Revisión de 15:27 20 oct 2010

1 Enunciado

Un punto material $P$ se mueve en el plano $O X Y$ describiendo una trayectoria parabólica de ecuación $y 2 = (b 2 / a) x$ . Se sabe que la partícula se halla inicialmente en reposo en la posición $x = a$ , $y = b$ ; y que la componente $y$ de su aceleración verifica en todo instante la expresión: $a y = - k 2 y$ (con k = cte). Determine en función del tiempo la posición, velocidad y aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?

2 Solución

El movimiento de la partícula puede descomponerse en sus componentes cartesianas

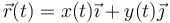
$\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}$

siendo la aceleración

$\vec{a}=\ddot{x}\vec{\imath}+\ddot{y}\vec{\jmath}$

En este caso conocemos la relación entre la componente vertical de la aceleración y la coordenada correspondiente

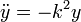
$\ddot{y}=-k^2y$

que nos dice que en la coordenada $y$ experimenta un movimiento armónico simple, con solución

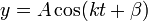
$y = A\cos(k t+\beta)\,$

Las constantes $A$ y $β$ las obtenemos de las condiciones iniciales. Sabemos que inicialmente la partícula se encuentra en $y = b$ y su velocidad inicial es nula, por lo que

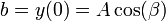
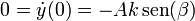
$b = y(0) = A\cos(\beta)\,$ $0 = \dot{y}(0) = -Ak\,\mathrm{sen}(\beta)$

de donde

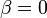
$\beta = 0\,$ $A=b\,$

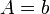
y la coordenada y en cada instante es

$y(t) = b\cos(k t)\,$

La coordenada $x$ la obtenemos de la ecuación de la parábola

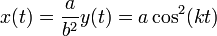
$x(t) = \frac{a}{b^2}y(t) = a\cos^2(k t)$

Aplicando relaciones trigonométricas, queda

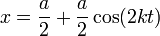
$x = \frac{a}{2}+\frac{a}{2}\cos(2kt)$

que nos dice, que la partícula también oscila armónicamente en la dirección horizontal, pero con frecuencia doble que en la vertical.

El vector de posición instantánea es

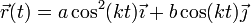
$\vec{r}(t) = a\cos^2(kt)\vec{\imath}+b\cos(k t)\vec{\jmath}$

A partir de la posición obtenemos la velocidad

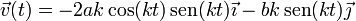
$\vec{v}(t) = -2ak\cos(kt)\,\mathrm{sen}(kt)\vec{\imath}-bk\,\mathrm{sen}(kt)\vec{\jmath}$

Volvemos a derivar respecto al tiempo, para obtener la aceleración

$\vec{a}(t)=2ak^2\left(\mathrm{sen}^2(kt)-\cos^2(kt)\right)\vec{\imath}-bk^2\cos(kt)\vec{\jmath}$

La siguiente posición de reposo se alcanza cuando la velocidad vuelve a ser nula. Separando las componentes de la velocidad

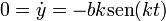
$0 = \dot{x}=-2ak\cos(kt)\mathrm{sen}(kt)$ $0 = \dot{y}=-bk\mathrm{sen}(kt)$

Estas dos componentes se anulan para

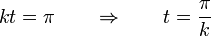
$kt = \pi\qquad\Rightarrow\qquad t = \frac{\pi}{k}$

y la posición en ese instante es

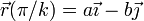
$\vec{r}(\pi/k) = a\vec{\imath}-b\vec{\jmath}$

que es la posición simétrica de la inicial respecto al eje de la parábola.

@@ Línea 37: / Línea 37: @@
 <center><math>x(t) = \frac{a}{b^2}y(t) = a\cos^2(k t)</math></center>
-Por tanto, el vector de posición instantánea es
+Aplicando relaciones trigonométricas, queda
+<center><math>x = \frac{a}{2}+\frac{a}{2}\cos(2kt)</math></center>
+que nos dice, que la partícula también oscila armónicamente en la dirección horizontal, pero con frecuencia doble que en la vertical.
+El vector de posición instantánea es
 <center><math>\vec{r}(t) = a\cos^2(kt)\vec{\imath}+b\cos(k t)\vec{\jmath}</math></center>

Partícula oscilando en parábola

De Laplace

Revisión de 15:27 20 oct 2010

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES