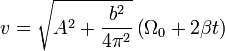Entrar Página Discusión Historial Go to the site toolbox

2.8. Ejemplo de movimiento helicoidal

De Laplace

(Diferencias entre revisiones)
(→Celeridad)
Línea 45: Línea 45:
con lo que
con lo que
-
<center><math>v = \sqrt{A^2+\frac{b^2}{4\pi^2}}(\Omega_0+2\beta t\right)</math></center>
+
<center><math>v = \sqrt{A^2+\frac{b^2}{4\pi^2}}\left(\Omega_0+2\beta t\right)</math></center>
==Aceleración tangencial==
==Aceleración tangencial==

Revisión de 08:57 6 oct 2010

Contenido

1 Enunciado

Una partícula se mueve a lo largo de la hélice descrita por la ecuación paramétrica

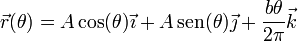
\vec{r}(\theta)=A\cos(\theta)\vec{\imath}+A\,\mathrm{sen}(\theta)\vec{\jmath}+\frac{b\theta}{2\pi}\vec{k}

donde A y b son constantes conocidas. El movimiento de la partícula sigue la ley horaria

θ(t) = Ω0t + βt2

donde Ω0 y β son constantes conocidas.

  1. Determine el parámetro arco de la hélice descrita, como función del parámetro θ y como función del tiempo.
  2. Halle la rapidez del movimiento.
  3. Calcule la componente tangencial de la aceleración de la partícula en todo instante.
  4. Para el instante t = 0 calcule la velocidad y la aceleración de la partícula.
  5. Para el mismo instante, halle los vectores del triedro de Frenet, así como el radio de curvatura de la partícula y su aceleración normal.

2 Parámetro arco

Podemos determinar el parámetro arco empleando la variable θ según la relación

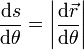
\frac{\mathrm{d}s}{\mathrm{d}\theta}=\left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|

Derivando y calculando el módulo

\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=-A\,\mathrm{sen}(\theta)\vec{\imath}+A\cos(\theta)\vec{\jmath}+\frac{b}{2\pi}\vec{k}

El módulo de este vector vale

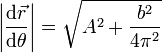
\left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|=\sqrt{A^2+\frac{b^2}{4\pi^2}}

Puesto que el módulo es independiente de θ, su integración es inmediata

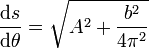
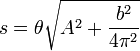
\frac{\mathrm{d}s}{\mathrm{d}\theta}=\sqrt{A^2+\frac{b^2}{4\pi^2}}   \Rightarrow    s=\theta\sqrt{A^2+\frac{b^2}{4\pi^2}}

3 Celeridad

Hallamos la rapidez por aplicación de la regla de la cadena

v=\frac{\mathrm{d}s}{\mathrm{d}t}=\frac{\mathrm{d}s}{\mathrm{d}\theta}\,\frac{\mathrm{d}\theta}{\mathrm{d}t}

El primer factor ya lo conocemos; para el segundo derivamos la expresión del enunciado

\frac{\mathrm{d}\theta}{\mathrm{d}t}=\Omega_0+2\beta t

con lo que

v = \sqrt{A^2+\frac{b^2}{4\pi^2}}\left(\Omega_0+2\beta t\right)

4 Aceleración tangencial

5 Velocidad y aceleración iniciales

6 Triedro de Frenet

Obtenido de "http://tesla.us.es/wiki/index.php/2.8._Ejemplo_de_movimiento_helicoidal"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace