Partícula oscilando en parábola
De Laplace
(→Solución) |
|||
| Línea 33: | Línea 33: | ||
<center><math>y(t) = b\cos(k t)\,</math></center> | <center><math>y(t) = b\cos(k t)\,</math></center> | ||
| - | La coordenada x la obtenemos de la ecuación de la parábola | + | La coordenada <math>x</math> la obtenemos de la ecuación de la parábola |
<center><math>x(t) = \frac{a}{b^2}y(t) = a\cos^2(k t)</math></center> | <center><math>x(t) = \frac{a}{b^2}y(t) = a\cos^2(k t)</math></center> | ||
| Línea 48: | Línea 48: | ||
<center><math>\vec{a}(t)=2ak^2\left(\mathrm{sen}^2(kt)-\cos^2(kt)\right)\vec{\imath}-bk^2\cos(kt)\vec{\jmath}</math></center> | <center><math>\vec{a}(t)=2ak^2\left(\mathrm{sen}^2(kt)-\cos^2(kt)\right)\vec{\imath}-bk^2\cos(kt)\vec{\jmath}</math></center> | ||
| + | |||
| + | La siguiente posición de reposo se alcanza cuando la velocidad vuelve a ser nula. Separando las componentes de la velocidad | ||
| + | |||
| + | <center><math>0 = \dot{x}=-2ak\cos(kt)\mathrm{sen}(kt)</math>{{qquad}}{{qquad}}<math>0 = \dot{y}=-bk\mathrm{sen}(kt)</math></center> | ||
| + | |||
| + | Estas dos componentes se anulan para | ||
| + | |||
| + | <center><math>kt = \pi\qquad\Rightarrow\qquad t = \frac{\pi}{k}</math></center> | ||
| + | |||
| + | y la posición en ese instante es | ||
| + | |||
| + | <center><math>\vec{r}(\pi/k) = a\vec{\imath}-b\vec{\jmath}</math></center> | ||
| + | |||
| + | que es la posición simétrica de la inicial respecto al eje de la parábola. | ||
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
Revisión de 17:24 5 oct 2010
1 Enunciado
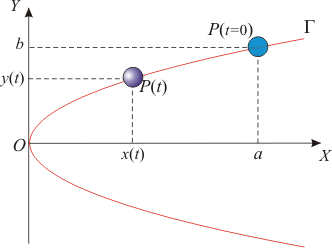
Un punto material P se mueve en el plano OXY describiendo una trayectoria parabólica de ecuación y2 = (b2 / a)x. Se sabe que la partícula se halla inicialmente en reposo en la posición x = a, y = b; y que la componente y de su aceleración verifica en todo instante la expresión: ay = − k2y (con k = cte). Determine en función del tiempo la posición, velocidad y aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?
2 Solución
El movimiento de la partícula puede descomponerse en sus componentes cartesianas
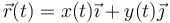
siendo la aceleración

En este caso conocemos la relación entre la componente vertical de la aceleración y la coordenada correspondiente
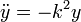
que nos dice que en la coordenada y experimenta un movimiento armónico simple, con solución
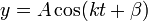
Las constantes A y β las obtenemos de las condiciones iniciales. Sabemos que inicialmente la partícula se encuentra en y = b y su velocidad inicial es nula, por lo que
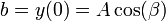
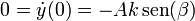
de donde
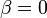
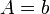
y la coordenada y en cada instante es

La coordenada x la obtenemos de la ecuación de la parábola
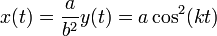
Por tanto, el vector de posición instantánea es
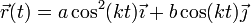
A partir de la posición obtenemos la velocidad
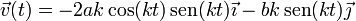
Volvemos a derivar respecto al tiempo, para obtener la aceleración

La siguiente posición de reposo se alcanza cuando la velocidad vuelve a ser nula. Separando las componentes de la velocidad

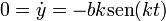
Estas dos componentes se anulan para
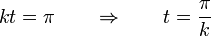
y la posición en ese instante es
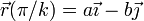
que es la posición simétrica de la inicial respecto al eje de la parábola.