Problemas de vectores libres (G.I.A.)
De Laplace
(→Componentes cartesianas de un vector) |
(→Diagonales_de_un_rombo) |
||
| Línea 8: | Línea 8: | ||
<math>\alpha=37.0^{\circ}</math> con el eje <math>+X</math>. Calcula también los ángulos con los ejes <math>X</math> e <math>Y</math>. | <math>\alpha=37.0^{\circ}</math> con el eje <math>+X</math>. Calcula también los ángulos con los ejes <math>X</math> e <math>Y</math>. | ||
| - | ==[[Diagonales_de_un_rombo_(G.I.A.)| | + | ==[[Diagonales_de_un_rombo_(G.I.A.)|Diagonales de un rombo]]== |
Usando el álgebra vectorial, demuestra que las diagonales de un rombo | Usando el álgebra vectorial, demuestra que las diagonales de un rombo | ||
Revisión de 12:53 5 oct 2010
Contenido |
1 Suma y diferencia de vectores
El vector 
tiene un módulo de 6.00 unidades y forma un ángulo de 
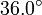con el eje X, mientras que el vector 
tiene un módulo de 7.00 unidades y apunta en la dirección negativa del eje X. Calcula la suma y la diferencia de estos dos vectores haciendo uso de los teoremas del seno y del coseno.
2 Componentes cartesianas de un vector
Calcula las componentes cartesianas de un vector con módulo de 13.0 unidades que forma un
ángulo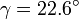 
con el eje Z y cuya proyección en el plano XY forma un ángulo
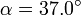con el eje + X. Calcula también los ángulos con los ejes X e Y.
3 Diagonales de un rombo
Usando el álgebra vectorial, demuestra que las diagonales de un rombo se cortan en ángulo recto.
4 Distancia mínima entre dos rectas
Hallar la menor distancia entre las rectas Δ(A,B) y Γ(C,D), y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas A(1, − 2, − 1) y B(4,0, − 3), para el caso de Δ, y C(1,2, − 1) y D(2, − 4, − 5), para la recta Γ.
