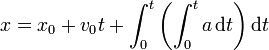Cinemática en una dimensión

De Laplace

(Diferencias entre revisiones)

Revisión de 22:38 1 oct 2010

Contenido

1 Introducción
2 Posición
3 Velocidad
- 3.1 Velocidad media
- 3.2 Velocidad instantánea
4 Aceleración
5 Tipos de movimiento rectilíneo
- 5.1 Uniforme
- 5.2 Uniformemente acelerado

1 Introducción

Antes de considerar el problema completo del movimiento de una partícula en el espacio de tres dimensiones, examinaremos el problema unidimensional, más simple, de una partícula que realiza un movimiento rectilíneo

2 Posición

Cuando tenemos una partícula cuyo movimiento se ciñe a una recta, no necesitamos el álgebra vectorial para identificar las diferentes posiciones de la partícula. Nos basta con una etiqueta $x (t)$ que designa la posición a lo largo de la recta. Esta cantidad tiene un signo que indica si nos encontramos a la izquierda o a la derecha de la posición a lo largo de la recta que hayamos etiquetado como $x = 0$ .

En el caso unidimensional podemos representar la posición frente al tiempo, colocando el tiempo en el eje de abscisas y la posición en el de ordenadas. Esta posibilidad no existe en el caso tridimensional.

Cuando una partícula cambia de posición pasando de encontrarse en $x 1$ en el instante $t 1$ a una posición $x 2$ en el instante $t 2$ se dice que en elintervalo de tiempo $Δ t = t 2 - t 1$ ha experimentado un desplazamiento

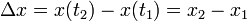
$\Delta x = x(t_2) - x(t_1) = x_2-x_1\,$

El desplazamiento que, como la posición, se mide en unidades de distancia (m, en el SI), posee la propiedad de que es independiente de que punto se toma como origen de posiciones.

3 Velocidad

3.1 Velocidad media

Si una partícula realiza un desplazamiento $Δ x$ en un intervalo $Δ t$ , se define la velocidad media (en una dimensión) como el cociente entre el desplazamiento y el intervalo empleado en realizarlo

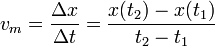
$v_m = \frac{\Delta x}{\Delta t} = \frac{x(t_2)-x(t_1)}{t_2-t_1}$

De la definición se desprende que:

Posee unidades de distancia dividida por tiempo, que en el sistema internacional serán m/s.
La velocidad media depende del desplazamiento neto entre dos puntos, por tanto si al final del intervalo la posición es la misma que al principio,, la velocidad media es 0, independientemente de las idas y vueltas que se hayan dado independientemente de la distancia que se haya recorrido.
La velocidad no es igual a espacio partido por tiempo, sino a un desplazamiento dividido por un intervalo, esto es, lo que cuenta no es el valor absoluto de la distancia o la hora que marca el reloj, sino cuánto ha cambiado la posición y cuánto tiempo se ha empleado en realizar dicho desplazamiento.
En la gráfica de la posición frente al tiempo, la velocidad media representa la pendiente de la recta secante que pasa por los puntos $(t 1, x 1)$ y $(t 2, x 2)$ . En particular si la posición inicial y la final son la misma, resulta una recta horizontal de pendiente nula.

3.2 Velocidad instantánea

El concepto de velocidad media no es especialmente útil, ya que solo nos informa del ritmo promedio, pero un movimiento concreto puede hacerse de forma irregular y normalmente interesa definir la velocidad en un momento dado, conocida como velocidad instantánea. Hoy día, con la presencia de velocímetros en los automóviles, el concepto de velocidad instantánea es intuitivo y todos tenemos una experiencia directa de la magnitud. Se trata de precisar matemáticamente el concepto.

Cuando decimos que en un instante dado la velocidad es de 120 km/h, ¿qué estamos diciendo exactamente? Evidentemente, no que durante la última hora se han recorrido 120 km, ya que igual sólo se llevan 10 minutos de marcha. Podríamos decir que durante el último minuto se han recorrido 2 km. ya que

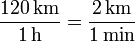
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}$

Esto ya es más preciso, pero aun no es del todo satisfactorio, ya que en un minuto hay tiempo suficiente a acelerar o frenar. Una mejor aproximación sería afirmar que en el último segundo se ha recorrido (1/30) km = 33.3 m. O podríamos decir que en la última décima de segundo se han recorrido 3.33 m,…

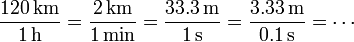
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}= \frac{33.3\,\mathrm{m}}{1\,\mathrm{s}}=\frac{3.33\,\mathrm{m}}{0.1\,\mathrm{s}}=\cdots$

En todos los casos la velocidad es de 120 km/h, pero cuanto más pequeño es el intervalo de tiempo considerado, más nos acercamos al ideal de medir la velocidad en un instante dado.

Definimos entonces la velocidad instantánea en una dimensión como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero (se reduce a un instante)

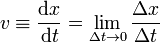
$v\equiv\frac{\mathrm{d}x}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}$

Matemáticamente, esto quiere decir que la velocidad instantánea es la derivada respecto al tiempo de la posición instantánea. En mecánica, una derivada respecto al tiempo suele representarse con un punto sobre la magnitud

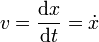
$v=\frac{\mathrm{d}x}{\mathrm{d}t} = \dot{x}$

De esta definición se deduce que:

Las unidades de la velocidad instantánea son la de una distancia dividida por un tiempo, en el SI m/s, aunque otras unidades como km/h son de uso frecuente.
La velocidad tiene un signo: es positiva si el valor de $x$ está aumentando (nos movemos hacia la derecha del punto de referencia) y es negativa si está disminuyendo (nos movemos hacia la izquierda).
La velocidad puede ser nula. En ese caso se dice que la partícula se encuentra en un estado de reposo instantáneo.
La velocidad no es igual al espacio partido por tiempo. Es la derivada de la posición respecto al tiempo.
En la gráfica de la posición frente al tiempo, la velocidad representa la pendiente de la recta tangente a la curva $x (t)$ en el punto $(t, x (t))$ .
Si el estado es de reposo instantáneo esta tangente es horizontal. En ese momento usualmente la posición alcanza un máximo o un mínimo.

Conocida la velocidad en cada instante y la posición inicial, puede hallarse la posición instantánea, sumando los desplazamientos infinitesimales, esto es, integrando

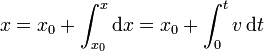
$x =x_0+\int_{x_0}^x \mathrm{d}x = x_0+\int_0^t v\,\mathrm{d}t$

Gráficamente, si trazamos la curva de la velocidad como función del tiempo, el desplazamiento desde la posición inicial es el área bajo la curva $v = v (t)$ .

4 Aceleración

La aceleración de un movimiento rectilíneo se define como la derivada de la velocidad instantánea, y por tanto, como la segunda derivada de la posición

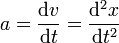
$a = \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}^2x}{\mathrm{d}t^2}$

Usando la notación de puntos para indicar la derivada respecto al tiempo

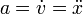
$a = \dot{v}=\ddot{x}$

De la definición se tiene que

La aceleración tiene dimensiones de longitud dividida por tiempo al cuadrado, siendo su unidad en el SI el m/s²
Una magnitud con dimensiones de aceleración que es especialmente importante es la aceleración de la gravedad en la superficie terrestre, cuyo valor estándar es, por definición,

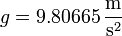
$g = 9.80665\,\frac{\mathrm{m}}{\mathrm{s}^2}$

de manera que muchas aceleraciones se expresan como múltiplos de esta unidad, aunque dichas aceleraciones no estén relacionadas con la gravedad. Así, por ejemplo, para medir las aceleraciones laterales de un piloto de Fórmula 1 en una curva se dice, por ejemplo, “está sometido a 3 fuerzas G”, que quiere decir que

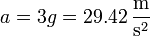
$a = 3g = 29.42\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Por tanto, g aquí funciona como unidad de medida de la aceleración.

En la gráfica $x (t)$ , la aceleración está asociada a la concavidad de la curva. Donde la aceleración es positiva la gráfica es cóncava hacia arriba, y donde es negativa es cóncava hacia abajo.

Conocida la aceleración en cada instante y la velocidad inicial, se puede hallar la velocidad en cada instante por integración de la aceleración

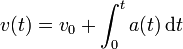
$v(t) = v_0 + \int_0^t a(t)\,\mathrm{d}t$

y la posición mediante la segunda integración

$x= x_0 + v_0 t + \int_0^t\left(\int_0^t a\,\mathrm{d}t\right)\mathrm{d}t$

@@ Línea 70: / Línea 70: @@
 <center><math>a = \dot{v}=\ddot{x}</math></center>
+De la definición se tiene que
+* La aceleración tiene dimensiones de longitud dividida por tiempo al cuadrado, siendo su unidad en el SI el m/s&sup2;
+* Una magnitud con dimensiones de aceleración que es especialmente importante es la aceleración de la gravedad en la superficie terrestre, cuyo valor estándar es, por definición,
+<center><math>g = 9.80665\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+: de manera que muchas aceleraciones se expresan como múltiplos de esta unidad, aunque dichas aceleraciones no estén relacionadas con la gravedad. Así, por ejemplo, para medir las aceleraciones laterales de un piloto de Fórmula 1 en una curva se dice, por ejemplo, &ldquo;está sometido a 3 fuerzas G&rdquo;, que quiere decir que
+<center><math>a = 3g = 29.42\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+:Por tanto, ''g'' aquí funciona como unidad de medida de la aceleración.
+* En la gráfica <math>x(t)</math>, la aceleración está asociada a la concavidad de la curva. Donde la aceleración es positiva la gráfica es cóncava hacia arriba, y donde es negativa es cóncava hacia abajo.
+Conocida la aceleración en cada instante y la velocidad inicial, se puede hallar la velocidad en cada instante por integración de la aceleración
+<center><math>v(t) = v_0 + \int_0^t a(t)\,\mathrm{d}t</math></center>
+y la posición mediante la segunda integración
+<center><math>x= x_0 + v_0 t + \int_0^t\left(\int_0^t a\,\mathrm{d}t\right)\mathrm{d}t</math></center>
 ===Tipos de movimiento rectilíneo===
 ====Uniforme====
 ====Uniformemente acelerado====

Cinemática en una dimensión

De Laplace

Revisión de 22:38 1 oct 2010

Contenido

1 Introducción

2 Posición

3 Velocidad

3.1 Velocidad media

3.2 Velocidad instantánea

4 Aceleración

5 Tipos de movimiento rectilíneo

5.1 Uniforme

5.2 Uniformemente acelerado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES