Entrar Página Discusión Historial Go to the site toolbox

2.1. Fórmulas potencialmente incorrectas

De Laplace

(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Página creada con '==Enunciado== De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de […')
Edición más nueva →

Revisión de 15:42 23 sep 2010

1 Enunciado

De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de análisis dimensional, R es una distancia y \vec{r} el vector de posición; t es el tiempo:

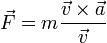
(a) \vec{F} = m\frac{\vec{v}\times\vec{a}}{\vec{v}}
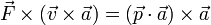
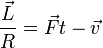
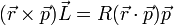
(b) \vec{F}\times(\vec{v}\times\vec{a}) = (\vec{p}\cdot\vec{a})\times\vec{a}
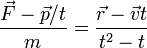
(c) \frac{\vec{L}}{R} = \vec{F}t-\vec{v}
(d) (\vec{r}\times\vec{p})\vec{L} = R(\vec{r}\cdot\vec{p})\vec{p}
(e) \frac{\vec{F}-\vec{p}/t}{m} = \frac{\vec{r}-\vec{v}t}{t^2-t}
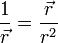
(f) \frac{1}{\vec{r}} = \frac{\vec{r}}{r^2}
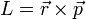
(g) L = \vec{r}\times\vec{p}
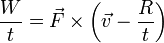
(h) \frac{W}{t} = \vec{F}\times\left(\vec{v}-\frac{R}{t}\right)

2 Caso (a)

La ecuación

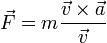
\vec{F} = m\frac{\vec{v}\times\vec{a}}{\vec{v}}

es obviamente incorrecta ya que no está definida la división por un vector. Por tanto, el segundo miembro es absurdo.

Obtenido de "http://tesla.us.es/wiki/index.php/2.1._F%C3%B3rmulas_potencialmente_incorrectas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace