Carga de un condensador parcialmente relleno

De Laplace

(Diferencias entre revisiones)

Revisión de 17:24 7 jun 2008

Contenido

1 Enunciado
2 Solución

1 Enunciado

Entre dos placas planas y paralelas separadas una distancia

a + b

se coloca una capa de espesor

a

de un medio de permitividad $\varepsilon$ y conductividad

σ

. El resto del espacio lo ocupa una capa de espesor

b

vacía.

En el instante $t = 0$ se conecta una diferencia de potencial $V 0$ .

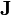¿Cuánto valen $\mathbf{E}$ , $\mathbf{D}$ y $\mathbf{J}$ inmediatamente después de conectar el potencial?
¿Cuánto valen un tiempo largo después de que se haya establecido?
¿Cuánto valen en cualquier instante?
¿Cómo varía, durante el periodo transitorio, la energía almacenada en el sistema? ¿Cuánta energía se disipa durante este periodo? ¿De dónde procede esta energía?
Si en lugar de una tensión escalón se aplica durante un largo periodo de tiempo un voltaje alterno V = V₀cos(ωt)
1. ¿Cuánto vale la corriente que llega al elemento? ¿Cuál es la impedancia del sistema? ¿Y el circuito equivalente?
2. ¿Cuanto vale la energía aportada por el generador en un periodo? ¿En qué se emplea esta energía?

2 Solución

Por la simetría del sistema, si despreciamos los efectos de borde, podemos admitir que los campos son uniformes en cada región aunque podrán, en principio, depender del tiempo.

Desde el instante $t = 0 +$ la diferencia de potencial entre las placas está fijada en $V_0$, por lo que siempre se verificará

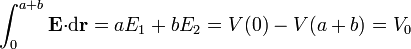
$\int_0^{a+b}\mathbf{E}{\cdot}\mathrm{d}\mathbf{r}=aE_1+bE_2=V(0)-V(a+b)=V_0$

Por otro lado, en la interfaz podrá haber una carga acumulada, lo que hace que el vector desplazamiento sea discontinuo

$\mathbf{n}{\cdot}[\mathbf{D}]=\sigma_s\quad\Rightarrow\quad \varepsilon_0E_2-\varepsilon E_1=\sigma_s$

Esta carga aparece debido a la presencia de conductividad en el medio, que posibilita que fluya carga por su interior. Esta carga acumulada es también una incógnita del problema. No conocemos cuanto vale, pero sí como varía, ya que la acumulación de carga verifica

$\mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial \sigma_s}{\partial t}\quad\Rightarrow\quad \sigma E_1=\frac{\partial \sigma_s}{\partial t}$

El sistema de ecuaciones resultante

$aE_1+bE_2=V_0\,$

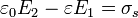
$\varepsilon_0E_2-\varepsilon E_1=\sigma_s\,$

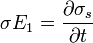
$\sigma E_1=\frac{\partial \sigma_s}{\partial t}$

posee solución en general, que se verá más adelante. Primero, consideraremos dos casos límite.

2.1 Campos inmediatamente después de la conexión

En el instante $t = 0 +$ , ya se han establecido los campos iniciales, pero aún no hay tiempo para la acumulación de carga en el interior del sistema. En este instante $\sigma_s=0$ y el sistema se reduce a

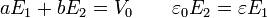
$aE_1+bE_2=V_0\qquad \varepsilon_0E_2=\varepsilon E_1\,$

La solución de este sistema es

$E_1=\frac{\varepsilon_0V_0}{\varepsilon b+\varepsilon_0 a} \qquad E_2=\frac{\varepsilon V_0}{\varepsilon b+\varepsilon_0 a}$

Esta distribución de campos es la misma que habría si los medios fueran dieléctricos perfectos.

El vector desplazamiento es, en las dos regiones,

$\mathbf{D}_1=\mathbf{D}_2=\frac{\varepsilon \varepsilon_0V_0}{\varepsilon b+\varepsilon_0 a}\mathbf{u}_z$

Las únicas cargas son las acumuladas en las placas. En la placa superior tenemos

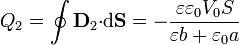
$Q_2=\oint \mathbf{D}_2{\cdot}\mathrm{d}\mathbf{S}=-\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}$

En la inferior la carga es la misma, salvo el signo

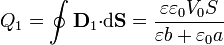
$Q_1=\oint \mathbf{D}_1{\cdot}\mathrm{d}\mathbf{S}=\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}$

En la interfaz no hay carga acumulada todavía.

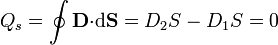
$Q_s=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=D_2 S-D_1S=0$

Aunque todavía no haya carga acumulada, ya está fluyendo corriente de una placa a través del material. La corriente en cada región es

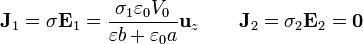
$\mathbf{J}_1=\sigma \mathbf{E}_1=\frac{\sigma_1\varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}\mathbf{u}_z\qquad\mathbf{J}_2=\sigma_2 \mathbf{E}_2= \mathbf{0}\,$

Al ser diferentes estas corrientes, la carga en la interfaz varía a un ritmo

$\left.\frac{\partial \sigma_s}{\partial t}\right|_{t=0^+}=-\mathbf{n}{\cdot}[\mathbf{J}]=J_1-J_2 =\frac{\sigma \varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}$

2.2 Campos en el estado estacionario

A medida que la carga se acumula en la interfaz, va produciendo un campo que se opone a la llegada de más carga. Finalmente se alcanza un estado estacionario en que la carga permanece constante. Para tiempos largos se cumple

$aE_1+bE_2=V_0\qquad \mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial \sigma_s}{\partial t}=0\quad\Rightarrow\quad \sigma E_1=\overbrace{\sigma_2}^{=0}E_2=0$

Puesto que en ningún momento hay corriente de conducción en la capa vacía, el estado estacionario se alcanza cuando también se anula corriente en el medio material. Como consecuencia de la ley de Ohm, también se anulará el campo en el medio

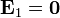
$\mathbf{E}_1=\mathbf{0}\,$

aunque no en la capa vacía

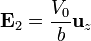
$\mathbf{E}_2 = \frac{V_0}{b}\mathbf{u}_z$

Vemos que en el estado estacionario, el sistema se ha reducido a un condensador de espesor $b$ , sometido a una diferencia de potencial $V 0$

El desplazamiento eléctrico en cada medio es

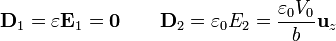
$\mathbf{D}_1=\varepsilon \mathbf{E}_1=\mathbf{0} \qquad \mathbf{D}_2=\varepsilon_0E_2=\frac{\varepsilon_0V_0}{b}\mathbf{u}_z$

La carga acumulada en la placa superior es

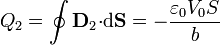
$Q_2=\oint \mathbf{D}_2{\cdot}\mathrm{d}\mathbf{S}= -\frac{\varepsilon_0V_0S}{b}$

mientras que en la inferior es

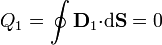
$Q_1=\oint \mathbf{D}_1{\cdot}\mathrm{d}\mathbf{S}=0$

La discontinuidad en $\mathbf{D}$ nos permite calcular la carga almacenada en la interfaz

$Q_s=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=\mathbf{n}{\cdot}[\mathbf{D}]S= \frac{\varepsilon_0 SV}{b}$

Vemos que lo que ocurre es que la carga se va desde la placa inferior hasta la interfaz, que es realmente la superficie exterior del conductor.

La densidad de corriente es ahora nula a través de todo el sistema y vale

$\mathbf{J}_1=\mathbf{J}_2=\mathbf{0}$

2.3 Evolución en el periodo transitorio

Debemos resolver las ecuaciones completas

$aE_1+bE_2=V_0 \qquad \varepsilon_0E_2-\varepsilon E_1=\sigma_s\qquad \sigma_1E_1=\frac{\partial \sigma_s}{\partial t}$

De las dos primeras ecuaciones se deduce que

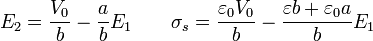
$E_2=\frac{V_0}{b}-\frac{a}{b}E_1 \qquad\sigma_s = \frac{\varepsilon_0V_0}{b}-\frac{\varepsilon b + \varepsilon_0a}{b}E_1$

Sustituyendo en la tercera

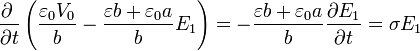
$\frac{\partial\ }{\partial t}\left(\frac{\varepsilon_0V_0}{b}-\frac{\varepsilon b + \varepsilon_0a}{b}E_1\right) = -\frac{\varepsilon b + \varepsilon_0a}{b}\frac{\partial E_1}{\partial t}= \sigma E_1$

La solución de esta ecuación diferencial es una exponencial decreciente

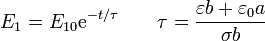
$E_1= E_{10} \mathrm{e}^{-t/\tau} \qquad \tau = \frac{\varepsilon b + \varepsilon_0a}{\sigma b}$

Nótese que el tiempo de decaimiento $τ$ no es igual a 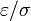$\varepsilon/\sigma$ , como podría pensarse ingenuamente.

El valor de la amplitud $E 10$ lo obtenemos de que conocemos el valor del campo justo después de la conexión

$E_{10} = \frac{\varepsilon_0V_0}{\varepsilon b + \varepsilon_0a} \qquad \mathbf{E} = \frac{\varepsilon_0V_0}{\varepsilon b + \varepsilon_0a} \mathrm{e}^{-t/\tau}\mathbf{u}_z$

Conocido el campo en el medio material, obtenemos el valor del campo en la capa vacía. Se compone de una parte estacionaria y de una parte transitoria que decae exponencialmente:

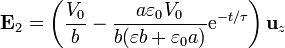
$\mathbf{E}_2 = \left(\frac{V_0}{b} - \frac{a\varepsilon_0V_0}{b(\varepsilon b + \varepsilon_0a)} \mathrm{e}^{-t/\tau}\right)\mathbf{u}_z$

Agrupando los términos, podemos escribir este campo como

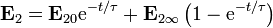
$\mathbf{E}_2 = \mathbf{E}_{20} \mathrm{e}^{-t/\tau} + \mathbf{E}_{2\infty} \left(1-\mathrm{e}^{-t/\tau}\right)$

esto es, el campo inicial decae exponencialmente, siendo sustituido por su valor final, que tiende exponencialmente a su valor estacionario.

Un análisis similar puede hacerse con la carga superficial, aunque en este caso su valor inicial es nulo:

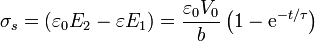
$\sigma_s = (\varepsilon_0E_2-\varepsilon E_1) = \frac{\varepsilon_0 V_0}{b}\left(1-\mathrm{e}^{-t/\tau}\right)$

2.4 Potencia y energía durante el periodo transitorio

2.4.1 Energía almacenada

Podemos calcular la energía almacenada en el condensador partir de la densidad de energía

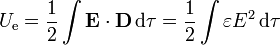
$U_\mathrm{e}=\frac{1}{2}\int \mathbf{E}\cdot\mathbf{D}\,\mathrm{d}\tau = \frac{1}{2}\int \varepsilon E^2\,\mathrm{d}\tau$

Teniendo en cuenta que el campo eléctrico es uniforme en cada región, esta integral equivale a la suma de dos términos

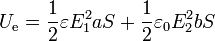
$U_\mathrm{e}=\frac{1}{2}\varepsilon E_1^2 a S + \frac{1}{2}\varepsilon_0 E_2^2 b S$

Sustituyendo las expresiones de los campos obtenemos el valor de la energía.

Justo después de la conexión ( $t = 0 +$ )

$U_\mathrm{e}(0^+) = \frac{\varepsilon\varepsilon_0 S V_0^2}{2(\varepsilon b + \varepsilon_0a)}$

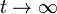Una vez que se alcanza el estado estacionario ( $t\to \infty$ )

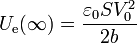
$U_\mathrm{e}(\infty) = \frac{\varepsilon_0 S V_0^2}{2b}$

Durante el periodo transitorio, la energía evoluciona del primer valor al segundo

$U_\mathrm{e}(t) = \frac{\varepsilon_0 S V_0^2}{2b}\left(1-\frac{a\varepsilon_0 \mathrm{e}^{-t/\tau}\left(2-\mathrm{e}^{-t/\tau}\right)}{\varepsilon b + \varepsilon_0a}\right)$

Durante el transitorio, la energía almacenada aumenta

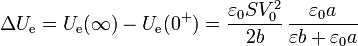
$\Delta U_\mathrm{e} = U_\mathrm{e}(\infty)-U_\mathrm{e}(0^+) = \frac{\varepsilon_0 S V_0^2}{2b}\,\frac{\varepsilon_0a}{\varepsilon b + \varepsilon_0a}$

2.4.2 Potencia y energía disipada

Durante el periodo transitorio se disipa energía en el medio óhmico, de acuerdo con la ley de Joule

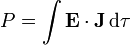
$P = \int \mathbf{E}\cdot\mathbf{J}\,\mathrm{d}\tau$

Teniendo en cuenta que en esta región el campo es uniforme, esta integral da

$P = \sigma a S E_1^2 = \frac{\sigma a S \varepsilon_0^2 V_0^2 \mathrm{e}^{-2t/\tau}}{(\varepsilon b + \varepsilon_0 a)^2}$

La energía total disipada en el medio óhmico será la integral de esta potencia

$W_d = \int_0^\infty P\,\mathrm{d}t = \frac{\sigma a S \varepsilon_0^2 V_0^2}{(\varepsilon b + \varepsilon_0 a)^2}\,\frac{\tau}{2}=\frac{a\varepsilon_0^2 SV_0^2}{2b(\varepsilon b + \varepsilon_0 a)}$

2.4.3 Balance energético

2.5 Comportamiento en corriente alterna

2.5.1 Corriente, impedancia y circuito equivalente

2.5.2 Energía en corriente alterna

@@ Línea 206: / Línea 206: @@
 La energía total disipada en el medio óhmico será la integral de esta potencia
-<center><math>W_d = \int_0^\infty P\,\mathrm{d}t = \frac{\sigma a S \varepsilon_0^2 V_0^2}{(\varepsilon b + \varepsilon_0 a)^2}\,\frac{\tau}{2}=\frac{a\varepsilon_0^2 SV_0^2}{b(\varepsilon b + \varepsilon_0 a)}</math></center>
+<center><math>W_d = \int_0^\infty P\,\mathrm{d}t = \frac{\sigma a S \varepsilon_0^2 V_0^2}{(\varepsilon b + \varepsilon_0 a)^2}\,\frac{\tau}{2}=\frac{a\varepsilon_0^2 SV_0^2}{2b(\varepsilon b + \varepsilon_0 a)}</math></center>
 ====Balance energético====

Carga de un condensador parcialmente relleno

De Laplace

Revisión de 17:24 7 jun 2008

Contenido

1 Enunciado

2 Solución

2.1 Campos inmediatamente después de la conexión

2.2 Campos en el estado estacionario

2.3 Evolución en el periodo transitorio

2.4 Potencia y energía durante el periodo transitorio

2.4.1 Energía almacenada

2.4.2 Potencia y energía disipada

2.4.3 Balance energético

2.5 Comportamiento en corriente alterna

2.5.1 Corriente, impedancia y circuito equivalente

2.5.2 Energía en corriente alterna

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES