1.4. Arco capaz
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 33: | Línea 33: | ||
Esta construcción es útil en Mecánica también en su sentido inverso. Imaginemos una escalera apoyada sobre una pared y el suelo. Cuando la escalera resbala, deslizándose sobre la pared y el suelo, ¿qué trayectoria describe el punto medio de la escalera? En este caso P es la esquina y A y B son los extremos de la escalera. C es su punto medio. Si L es la longitud de la escalera, este resultado prueba que <math>|\overrightarrow{PC}| = L/2</math> y por tanto el punto C describe un arco de circunferencia. | Esta construcción es útil en Mecánica también en su sentido inverso. Imaginemos una escalera apoyada sobre una pared y el suelo. Cuando la escalera resbala, deslizándose sobre la pared y el suelo, ¿qué trayectoria describe el punto medio de la escalera? En este caso P es la esquina y A y B son los extremos de la escalera. C es su punto medio. Si L es la longitud de la escalera, este resultado prueba que <math>|\overrightarrow{PC}| = L/2</math> y por tanto el punto C describe un arco de circunferencia. | ||
| - | + | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | |
| - | [[Categoría:Problemas de | + | |
Revisión de 14:58 19 sep 2010
1 Enunciado
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores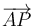 
y 
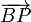son ortogonales.
Inversamente, sean A, B y P tres puntos tales que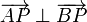 
. Sea C el punto medio entre A y B. Pruebe que 
.
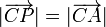2 Solución
Para ver que son ortogonales calculamos el producto escalar de los dos vectores.
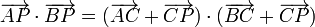
Desarrollando en esta expresión
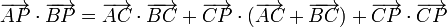
Ahora bien, por ser puntos diametralmente opuestos,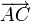 
y 
son vectores del mismo módulo R, misma dirección y sentido contrario, por lo que
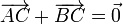
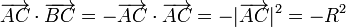
lo que nos lleva a
El producto escalar es nulo y los vectores son, por tanto, ortogonales.
La demostración del enunciado recíproco es la misma, pero recorrida en sentido inverso.
El resultado es independiente del punto P, siempre que se encuentre sobre la circunferencia. A esta construcción se la denomina arco capaz.
Esta construcción es útil en Mecánica también en su sentido inverso. Imaginemos una escalera apoyada sobre una pared y el suelo. Cuando la escalera resbala, deslizándose sobre la pared y el suelo, ¿qué trayectoria describe el punto medio de la escalera? En este caso P es la esquina y A y B son los extremos de la escalera. C es su punto medio. Si L es la longitud de la escalera, este resultado prueba que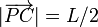 
y por tanto el punto C describe un arco de circunferencia.
