1.4. Arco capaz
De Laplace
(Diferencias entre revisiones)
(→Paralelogramo en trapezoide) |
|||
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
| + | Sean <math>A</math> y <math>B</math> dos puntos diametralmente opuestos en una circunferencia c. Sea <math>P</math> otro punto de la misma circunferencia. Demuestre que los vectores <math>\overrightarrow{AP}</math> y <math>\overrightarrow{BP}</math> son ortogonales. | ||
| + | Inversamente, sean <math>A</math>, <math>B</math> y <math>P</math> tres puntos tales que <math>\overrightarrow{AP} \perp \overrightarrow{BP}</math>. Sea <math>C</math> el punto medio entre <math>A</math> y <math>B</math>. Pruebe que <math>|\overrightarrow{CP}| = |\overrightarrow{CA}|</math>. | ||
| + | |||
| + | ==Solución== | ||
| + | |||
| + | [[Categoría:Problemas de álgebra vectorial (G.I.T.I.)]] | ||
Revisión de 07:58 16 sep 2010
1 Enunciado
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores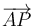 
y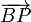 
son ortogonales.
Inversamente, sean A, B y P tres puntos tales que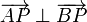 
. Sea C el punto medio entre A y B. Pruebe que 
.
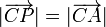