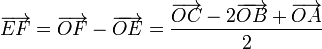1.2. Paralelogramo en cuadrilátero
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogr…') |
|||
| Línea 4: | Línea 4: | ||
==Solución== | ==Solución== | ||
| + | Sea O el origen de coordenadas. En ese caso los vectores de posición de los vértices son <math>\overrightarrow{OA}</math>, <math>\overrightarrow{OB}</math>, <math>\overrightarrow{OC}</math> y <math>\overrightarrow{OD}</math>. Las posiciones de los puntos medios E, F, G y H se encuentran en | ||
| + | |||
| + | <center><math>\overrightarrow{OE}=\frac{\overrightarrow{OA}+\overrightarrow{OB}}{2}</math>{{qquad}}{{qquad}}<math>\overrightarrow{OF}=\frac{\overrightarrow{OB}+\overrightarrow{OC}}{2}</math>{{qquad}}{{qquad}}<math>\overrightarrow{OG}=\frac{\overrightarrow{OC}+\overrightarrow{OD}}{2}</math>{{qquad}}{{qquad}}<math>\overrightarrow{OH}=\frac{\overrightarrow{OD}+\overrightarrow{OA}}{2}</math></center> | ||
| + | |||
| + | Para demostrar que estos cuatro puntos forman un paralelogramo, debemos probar que sus lados son paralelos dos a dos. El vector que une E y F es | ||
| + | |||
| + | <center><math>\overrightarrow{EF}=\overrightarrow{OF}-\overrightarrow{OE}=\frac{\overrightarrow{OC}-2\overrightarrow{OB}+\overrightarrow{OA}}{2}</math></center> | ||
[[Categoría:Problemas de álgebra vectorial (G.I.T.I.)]] | [[Categoría:Problemas de álgebra vectorial (G.I.T.I.)]] | ||
Revisión de 00:24 16 sep 2010
1 Enunciado
Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogramo.
2 Solución
Sea O el origen de coordenadas. En ese caso los vectores de posición de los vértices son 
, 
, 
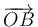y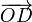 
. Las posiciones de los puntos medios E, F, G y H se encuentran en
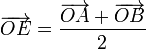
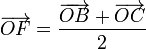
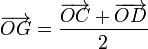
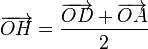
Para demostrar que estos cuatro puntos forman un paralelogramo, debemos probar que sus lados son paralelos dos a dos. El vector que une E y F es
