Problemas de cinemática del sólido rígido (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Velocidad de tres puntos de un sólido) |
(→Velocidad de tres puntos de un sólido) |
||
| Línea 28: | Línea 28: | ||
# Determine la posición del eje instantáneo de rotación y mínimo deslizamiento. | # Determine la posición del eje instantáneo de rotación y mínimo deslizamiento. | ||
| - | ==Triángulo en movimiento helicoidal | + | ==[[Triángulo en movimiento helicoidal]]== |
El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos: | El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos: | ||
| Línea 34: | Línea 34: | ||
* El vértice C se mueve describiendo la hélice <math>\Gamma</math>, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde <math>R</math> y <math>h</math> son constantes conocidas): | * El vértice C se mueve describiendo la hélice <math>\Gamma</math>, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde <math>R</math> y <math>h</math> son constantes conocidas): | ||
| - | <center><math>\vec{r}(\theta | + | <center><math>\vec{r}(\theta)= R\cos\theta\vec{\imath}+R\,\mathrm{sen}\,\theta\vec{\jmath}+ h\theta\vec{k}</math></center> |
# Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado. | # Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado. | ||
Revisión de 16:03 3 ago 2010
1 Ejemplo de campo de velocidades de un sólido
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,
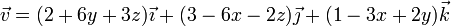
- Pruebe que corresponde al movimiento de un sólido rígido.
- Determine la velocidad angular y la velocidad de deslizamiento.
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.
2 Velocidad de tres puntos de un sólido
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
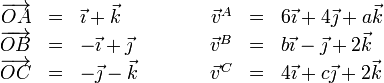
- Halle los valores de a, b, c.
- Halle la velocidad del punto
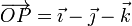 .
.
- Calcule la velocidad angular y la de deslizamiento
- Determine la posición del eje instantáneo de rotación y mínimo deslizamiento.
3 Triángulo en movimiento helicoidal
El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos:
- Los vértices A y B permanecen en todo instante sobre el eje OZ, desplazándose ambos con igual velocidad instantánea:
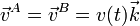 .
.
- El vértice C se mueve describiendo la hélice Γ, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde R y h son constantes conocidas):

- Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado.
- Exprese la componente normal de la aceleración del vértice C en un instante cualquiera, en función de los datos del enunciado.
- Para el caso en que v(t) = v0 (cte.), y h = R / 2, calcule la aceleración del vértice C. Determine la ley horaria s = s(t) con que el punto C describe su trayectoria.





